Polymer in water¶
Solvating and stretching a small polymer molecule
The goal of this tutorial is to use LAMMPS and solvate a small hydrophilic polymer (PEG - PolyEthylene Glycol) in a reservoir of water.
An all-atom description is used for both PEG (GROMOS 54A7 force field [24]) and water (SPC flexible model [25]) and the long range Coulomb interactions are solved using the PPPM solver [26]. Once the water reservoir is properly equilibrated at the desired temperature and pressure, the polymer molecule is added and a constant stretching force is applied to both ends of the polymer. The evolution of the polymer length is measured as a function of time.
This tutorial was inspired by a publication by Liese and coworkers, in which molecular dynamics simulations are compared with force spectroscopy experiments [27].
If you are completely new to LAMMPS, I recommend that you follow this tutorial on a simple Lennard-Jones fluid first.
You can support this webpage and access a dedicated discord channel
See the Contact me page.
This tutorial is compatible with the 2Aug2023 LAMMPS version.
Preparing the water reservoir¶
In this tutorial, the water reservoir is first prepared in the absence of polymer. A rectangular box of water is created and equilibrated at ambient temperature and ambient pressure. The SPC/Fw water model is used [25], which is a flexible variant of the rigid SPC (simple point charge) model [28].
Create a folder named pureH2O/. Inside this folder, create an empty text file named input.lammps. Copy the following lines in it:
units real
atom_style full
bond_style harmonic
angle_style harmonic
dihedral_style harmonic
pair_style lj/cut/coul/long 12
kspace_style pppm 1e-5
special_bonds lj 0.0 0.0 0.5 coul 0.0 0.0 1.0 angle yes
With the unit style real, masses are in grams per mole, distances in Ångstroms, time in femtoseconds, energies in Kcal/mole. With the atom_style full, each atom is a dot with a mass and a charge that can be linked by bonds, angles, dihedrals and/or impropers. The bond_style, angle_style, and dihedral_style commands define the potentials for the bonds, angles, and dihedrals used in the simulation, here harmonic.
Always refer to the LAMMPS documentation if you have doubts about the potential used by LAMMPS. For instance, this page gives the expression for the harmonic angular potential.
Finally, the special_bonds command cancels the Lennard-Jones interactions between the closest atoms of the same molecule.
About special bonds
Usually, molecular dynamics force fields are parametrized assuming that the first neighbors within a molecule do not interact directly through LJ or Coulomb potential. Here, since we use lj 0.0 0.0 0.5 and coul 0.0 0.0 1.0, the first and second neighbors in a molecule only interact through direct bond interactions. For the third neighbor (here third neighbor only concerns the PEG molecule, not the water), only half of the LJ interaction will be taken into account, and the full Coulomb interaction will be used.
With the pair_style named lj/cut/coul/long, atoms interact through both a Lennard-Jones (LJ) potential and Coulombic interactions. The value of \(12\,\text{Å}\) is the cutoff.
About cutoff in molecular dynamics
The cutoff of \(12\,\text{Å}\) applies to both LJ and Coulombic interactions, but in a different way. For LJ cut interactions, atoms interact with each other only if they are separated by a distance smaller than the cutoff. For Coulombic long, interactions between atoms closer than the cutoff are computed directly, and interactions between atoms outside that cutoff are computed in the reciprocal space.
Finally, the kspace command defines the long-range solver for the (long) Coulombic interactions. The pppm style refers to particle-particle particle-mesh.
About PPPM
Extracted from Luty and van Gunsteren: The PPPM method is based on separating the total interaction between particles into the sum of short-range interactions, which are computed by direct particle-particle summation, and long-range interactions, which are calculated by solving Poisson’s equation using periodic boundary conditions (PBCs) [26].
Then, let us create a 3D simulation box of dimensions \(9 \times 3 \times 3 \; \text{nm}^3\), and make space for 9 atom types (2 for the water molecule, and 7 for the polymer molecule), 7 bond types, 8 angle types, and 4 dihedral types. Copy the following lines into input.lammps:
region box block -45 45 -15 15 -15 15
create_box 9 box &
bond/types 7 &
angle/types 8 &
dihedral/types 4 &
extra/bond/per/atom 3 &
extra/angle/per/atom 6 &
extra/dihedral/per/atom 10 &
extra/special/per/atom 14
About extra per atom commands
The extra/x/per/atom commands are here for memory allocation. These commands ensure that enough memory space is left for a certain number of attributes for each atom. We won’t worry about those commands in this tutorial, just keep that in mind if one day you see the following error message ERROR: Molecule topology/atom exceeds system topology/atom.
Let us create a PARM.lammps file containing all the parameters (masses, interaction energies, bond equilibrium distances, etc). In input.lammps, add the following line:
include ../PARM.lammps
Then, download and save the parameter file next to the pureH2O/ folder.
Within PARM.lammps, the mass and pair_coeff of atoms of types 8 and 9 are for water and the atoms of types 1 to 7 are for the polymer molecule. Similarly, the bond_coeff 7 and angle_coeff 8 are for water, while all the other parameters are for the polymer.
Let us create water molecules. To do so, let us define what a water molecule is using a molecule template called H2O-SPCFw.mol, and then randomly create 1050 molecules. Add the following lines into input.lammps:
molecule h2omol H2O-SPCFw.mol
create_atoms 0 random 1050 87910 NULL mol &
h2omol 454756 overlap 1.0 maxtry 50
The overlap 1 option of the create_atoms command ensures that no atoms are placed exactly in the same position, as this would cause the simulation to crash. The maxtry 50 asks LAMMPS to try at most 50 times to insert the molecules, which is useful in case some insertion attempts are rejected due to overlap. In some cases, depending on the system and the values of overlap and maxtry, LAMMPS may not create the desired number of molecules. Always check the number of created atoms in the log file after starting the simulation:
Created 1050 atoms
When LAMMPS fails to create the desired number of molecules, a WARNING appears in the log file.
The molecule template named H2O-SPCFw.mol can be downloaded and saved in the pureH2O/ folder. This template contains the necessary structural information of a water molecule, such as the number of atoms, the id of the atoms that are connected by bonds, by angles, etc.
Then, let us organize the atoms of types 8 and 9 of the water molecules in a group named H2O and perform a small energy minimization. The energy minimization is mandatory here given the small overlap value of 1 Ångstrom chosen in the create_atoms command. Add the following lines to input.lammps:
group H2O type 8 9
minimize 1.0e-4 1.0e-6 100 1000
reset_timestep 0
The reset_timestep command is optional. It is used here because the minimize command is usually performed over an arbitrary number of steps.
Let us use the fix npt to control both the temperature and the pressure of the system, by adding the following line to input.lammps:
fix mynpt all npt temp 300 300 100 iso 1 1 1000
The fix npt allows us to impose both a temperature of \(300\,\text{K}\) (with a damping constant of \(100\,\text{fs}\)), and a pressure of 1 atmosphere (with a damping constant of \(1000\,\text{fs}\)). With the iso keyword, the three dimensions of the box will be re-scaled simultaneously.
Let us print the atom positions in a .lammpstrj file every 1000 steps (i.e. 1 ps), print the temperature volume, and density every 100 steps in 3 separate data files, and print the information in the terminal every 1000 steps:
dump mydmp all atom 1000 dump.lammpstrj
variable mytemp equal temp
variable myvol equal vol
fix myat1 all ave/time 10 10 100 v_mytemp file temperature.dat
fix myat2 all ave/time 10 10 100 v_myvol file volume.dat
variable myoxy equal count(H2O)/3
variable mydensity equal ${myoxy}/v_myvol
fix myat3 all ave/time 10 10 100 v_mydensity file density.dat
thermo 1000
The variable myoxy corresponds to the number of atoms divided by 3, i.e. the number of molecules.
On calling variables in LAMMPS
Both dollar sign and underscore can be used to call a previously defined variable. With the dollar sign, the initial value of the variable is returned, while with the underscore, the instantaneous value of the variable is returned. To probe the temporal evolution of a variable with time, the underscore must be used.
Finally, let us set the timestep to 1.0 fs, and run the simulation for 20 ps by adding the following lines to input.lammps:
timestep 1.0
run 20000
write_data H2O.data
The final state is written into H2O.data.
If you open the dump.lammpstrj file using VMD, you should see the system quickly reaching its equilibrium volume and density.
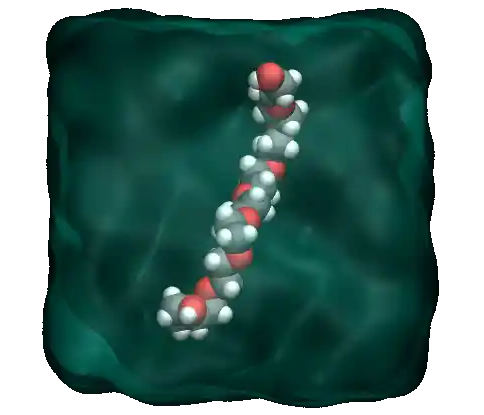
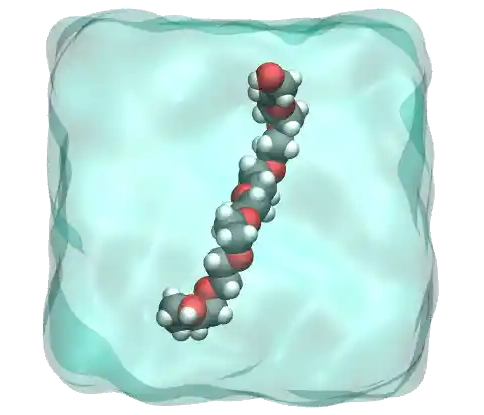
Figure: Water reservoir after equilibration. Oxygen atoms are in red, and hydrogen atoms are in white.
You can also open the density.dat file to ensure that the system converged toward an equilibrated liquid water system during the 20 ps of simulation.
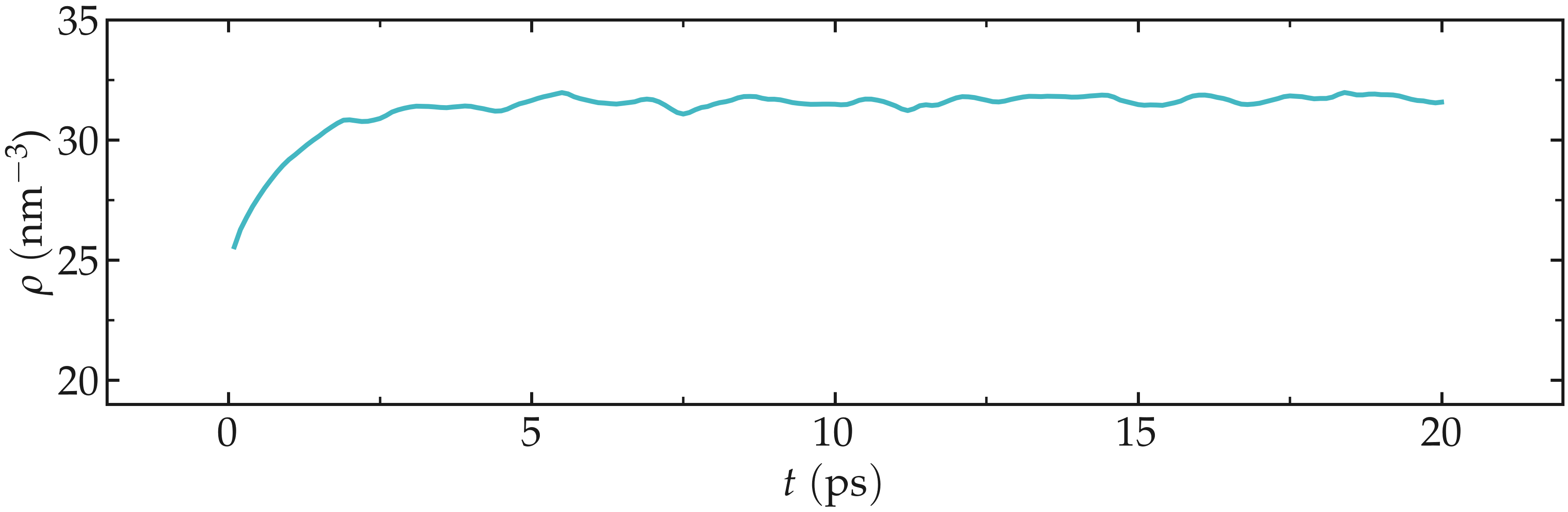
Figure: Evolution of the density of water with time. The density \(\rho\) reaches a plateau after \(\approx 10\,\text{ps}\).
If needed, you can download the water reservoir I have equilibrated and use it to continue with the tutorial.
Solvating the PEG in water¶
Once the water reservoir is equilibrated, we can safely include the PEG polymer in the water before performing the pull experiment on the polymer.
The PEG molecule topology was downloaded from the ATB repository [29, 30]. It has a formula \(\text{C}_{28}\text{H}_{58}\text{O}_{15}\), and the parameters are taken from the GROMOS 54A7 force field [24].
The PEG molecule
Figure: The PEG molecule in a vacuum. The carbon atoms are in gray, the oxygen atoms in red, and the hydrogen atoms in white.
Create a second folder alongside pureH2O/ and call it mergePEGH2O/. Create a new blank file in it, called input.lammps. Within input.lammps, copy the same first lines as previously:
units real
atom_style full
bond_style harmonic
angle_style harmonic
dihedral_style harmonic
pair_style lj/cut/coul/long 12
kspace_style pppm 1e-5
special_bonds lj 0.0 0.0 0.5 coul 0.0 0.0 1.0 angle yes dihedral yes
Then, import the previously generated data file H2O.data as well as the PARM.lammps file:
read_data ../pureH2O/H2O.data &
extra/bond/per/atom 3 &
extra/angle/per/atom 6 &
extra/dihedral/per/atom 10 &
extra/special/per/atom 14
include ../PARM.lammps
Let us create a molecule called pegmol from the molecule template for the PEG molecule, and let us create a single molecule in the middle of the box:
molecule pegmol PEG-GROMOS.mol
create_atoms 0 single 0 0 0 mol pegmol 454756
Let us create 2 groups to differentiate the PEG from the H2O, by adding the following lines to input.lammps:
group H2O type 8 9
group PEG type 1 2 3 4 5 6 7
Water molecules that are overlapping with the PEG must be deleted to avoid future crashing. Add the following line to input.lammps:
delete_atoms overlap 2.0 H2O PEG mol yes
Here, the value of 2 Ångstroms for the overlap cutoff was fixed arbitrarily and can be chosen through trial and error. If the cutoff is too small, the simulation will crash. If the cutoff is too large, too many water molecules will unnecessarily be deleted.
Finally, let us use the fix npt to control the temperature, as well as the pressure by allowing the box size to be rescaled along the x axis:
fix mynpt all npt temp 300 300 100 x 1 1 1000
timestep 1.0
Once more, let us dump the atom positions as well as the system temperature and volume:
dump mydmp all atom 100 dump.lammpstrj
thermo 100
variable mytemp equal temp
variable myvol equal vol
fix myat1 all ave/time 10 10 100 v_mytemp file temperature.dat
fix myat2 all ave/time 10 10 100 v_myvol file volume.dat
Let us also print the total enthalpy:
variable myenthalpy equal enthalpy
fix myat3 all ave/time 10 10 100 v_myenthalpy file enthalpy.dat
Finally, let us perform a short equilibration and print the final state in a data file. Add the following lines to the data file:
run 30000
write_data mix.data
If you open the dump.lammpstrj file using VMD, or have a look at the evolution of the volume in volume.dat, you should see that the box dimension slightly evolves along x to accommodate the new configuration.
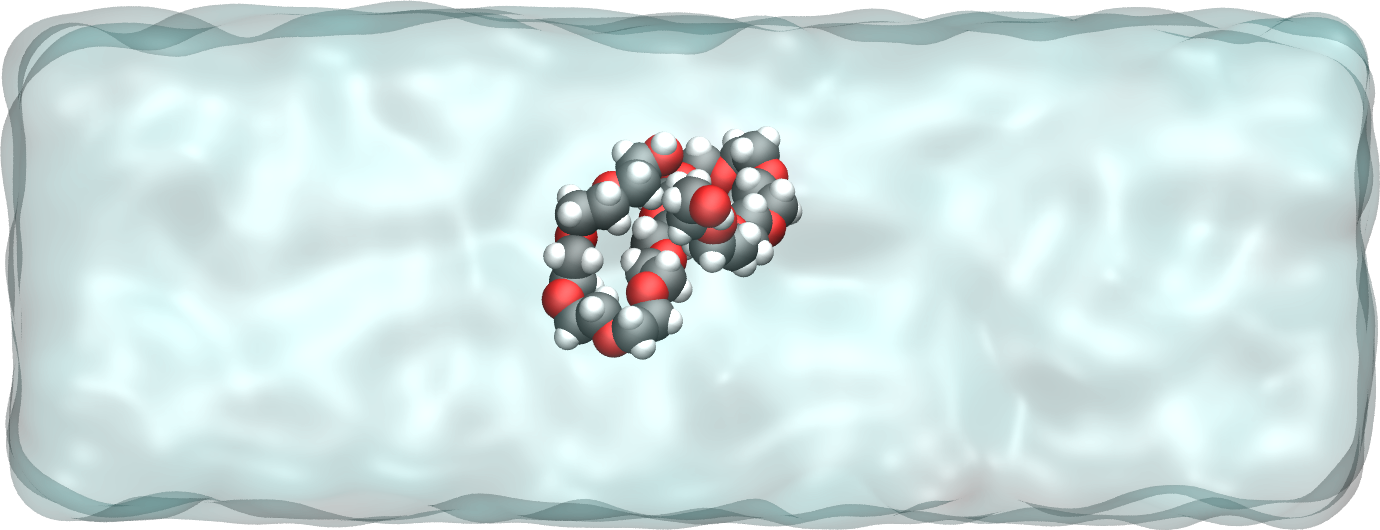
Figure: A single PEG molecule in water. Water molecules are represented as a transparent continuum field for clarity.
Stretching the PEG molecule¶
Here, a constant forcing is applied to the two ends of the PEG molecule until it stretches. Create a new folder next to the 3 previously created folders, call it pullonPEG/ and create a new input file in it called input.lammps.
First, let us create a variable f0 corresponding to the magnitude of the force we are going to apply. The force magnitude is chosen to be large enough to overcome the thermal agitation and the entropic contribution from both water and PEG molecules (it was chosen by trial and error). Copy in the input.lammps file:
variable f0 equal 5
Note that \(1\,\text{kcal/mol/Å}\) corresponds to \(67.2\,\text{pN}\). Then, copy the same lines as previously:
units real
atom_style full
bond_style harmonic
angle_style harmonic
dihedral_style harmonic
pair_style lj/cut/coul/long 12
kspace_style pppm 1e-5
special_bonds lj 0.0 0.0 0.5 coul 0.0 0.0 1.0 angle yes dihedral yes
Start the simulation from the equilibrated PEG-water system and include again the parameter file by adding the following lines to the input.lammps:
read_data ../mergePEGH2O/mix.data
include ../PARM.lammps
Then, let us create 4 atom groups: H2O and PEG (as previously), as well as 2 groups containing only the 2 oxygen atoms of types 6 and 7, respectively. Atoms of types 6 and 7 correspond to the oxygen atoms located at the ends of the PEG molecule, which we are going to use to pull on the PEG molecule. Add the following lines to the input.lammps:
group H2O type 8 9
group PEG type 1 2 3 4 5 6 7
group topull1 type 6
group topull2 type 7
Let us add the dump command again to print the atom positions:
dump mydmp all atom 1000 dump.lammpstrj
Let us use a simple thermostating for all atoms by adding the following lines to input.lammps:
timestep 1.0
fix mynvt all nvt temp 300 300 100
Let us also print the end-to-end distance of the PEG, here defined as the distance between the groups topull1 and topull2, as well as the temperature of the system by adding the following lines to input.lammps:
variable mytemp equal temp
fix myat1 all ave/time 10 10 100 v_mytemp file output-temperature.dat
variable x1 equal xcm(topull1,x)
variable x2 equal xcm(topull2,x)
variable y1 equal xcm(topull1,y)
variable y2 equal xcm(topull2,y)
variable z1 equal xcm(topull1,z)
variable z2 equal xcm(topull2,z)
variable delta_r equal sqrt((v_x1-v_x2)^2+(v_y1-v_y2)^2+(v_z1-v_z2)^2)
fix myat2 all ave/time 10 10 100 v_delta_r &
file output-end-to-end-distance.dat
thermo 1000
Finally, let us simulate 30 picoseconds without any external forcing:
run 30000
This first run serves as a benchmark to quantify the changes induced by the forcing. Then, let us apply a forcing on the 2 oxygen atoms using two add_force commands, and run for an extra 30 ps:
fix myaf1 topull1 addforce ${f0} 0 0
fix myaf2 topull2 addforce -${f0} 0 0
run 30000
If you open the dump.lammpstrj file using VMD, you should see that the PEG molecule eventually aligns in the direction of the force.
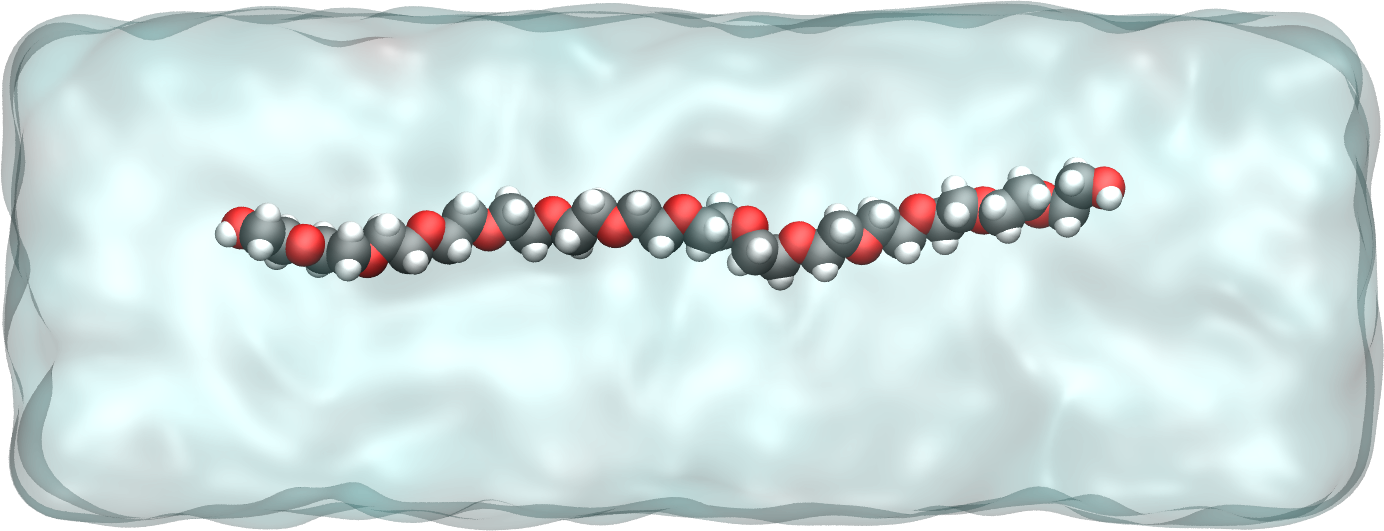
Figure: PEG molecule stretched along the x direction in water. Water molecules are represented as a transparent continuum field for clarity. See the corresponding video.
The evolution of the end-to-end distance over time shows the PEG adjusting to the external forcing:
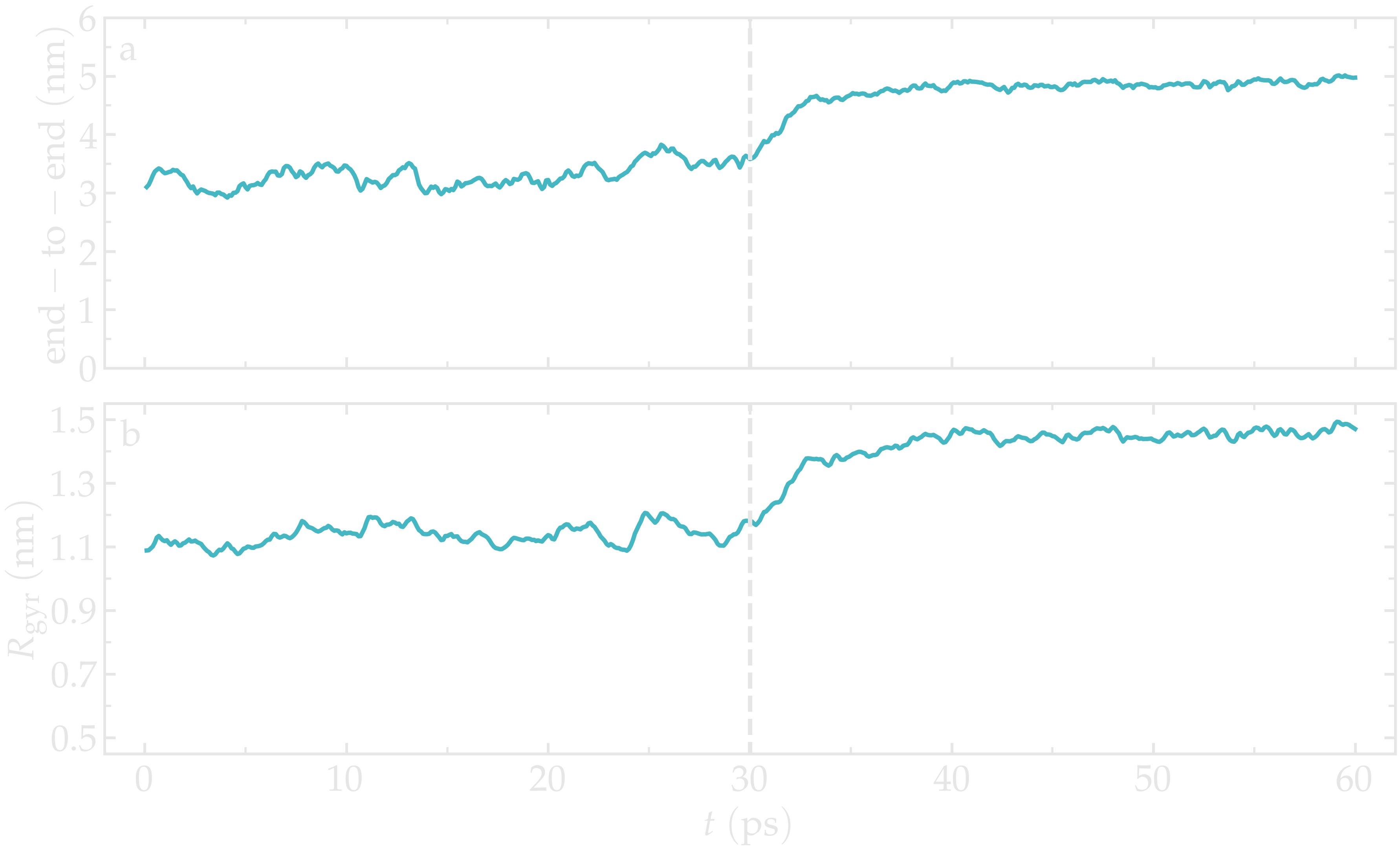
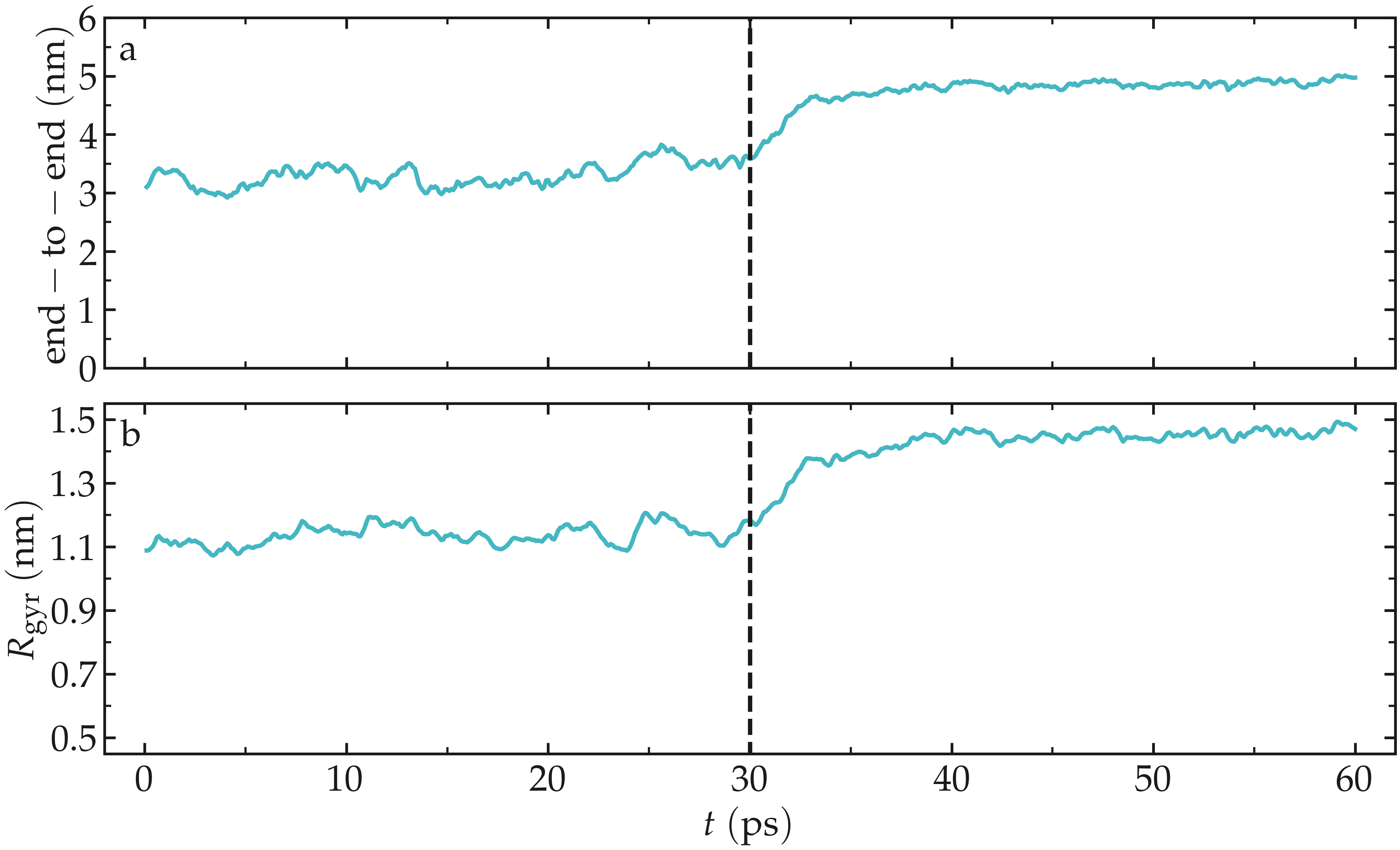
Figure: Evolution of the end-to-end distance of the PEG molecule with time. The forcing starts at \(t = 30\) ps.
There is a follow-up to this polymer in water tutorial as MDAnalysis tutorials, where the trajectory is imported in Python using MDAnalysis.
You can access the input scripts and data files that are used in these tutorials from this Github repository. This repository also contains the full solutions to the exercises.
Going further with exercises¶
Each comes with a proposed solution, see Solutions to the exercises.
Extract the radial distribution function¶
Extract the radial distribution functions (RDF or \(g(r)\)) between the oxygen atom of the water molecules and the oxygen atom from the PEG molecule. Compare the rdf before and after the force is applied to the PEG.
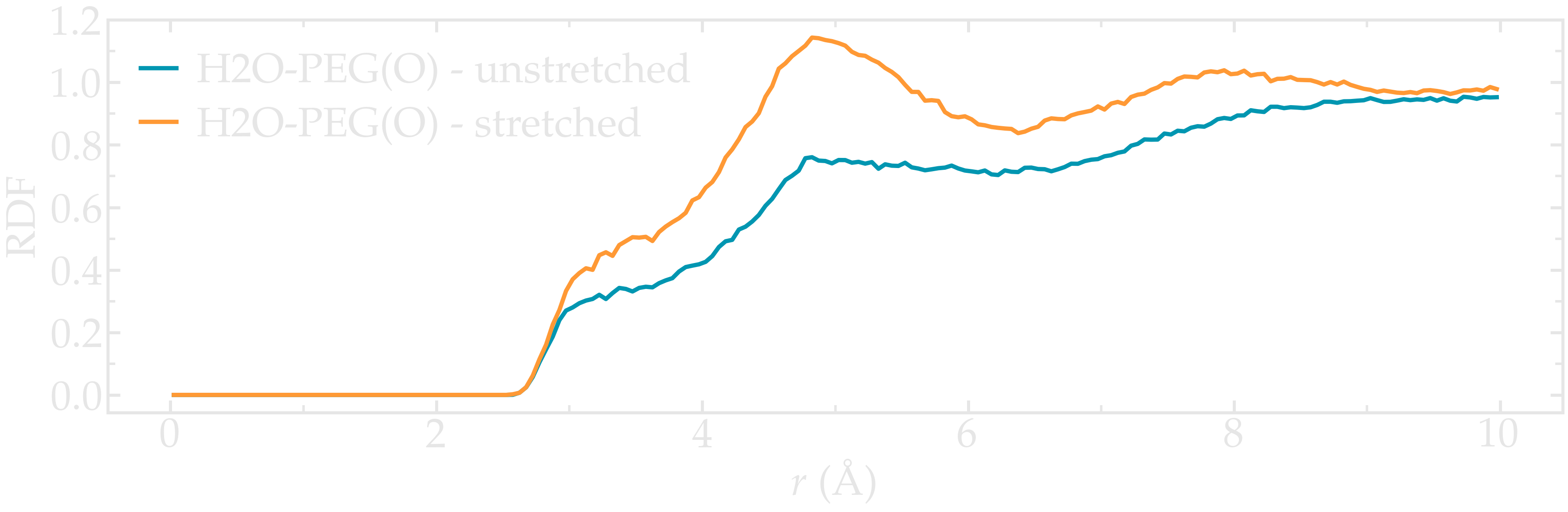
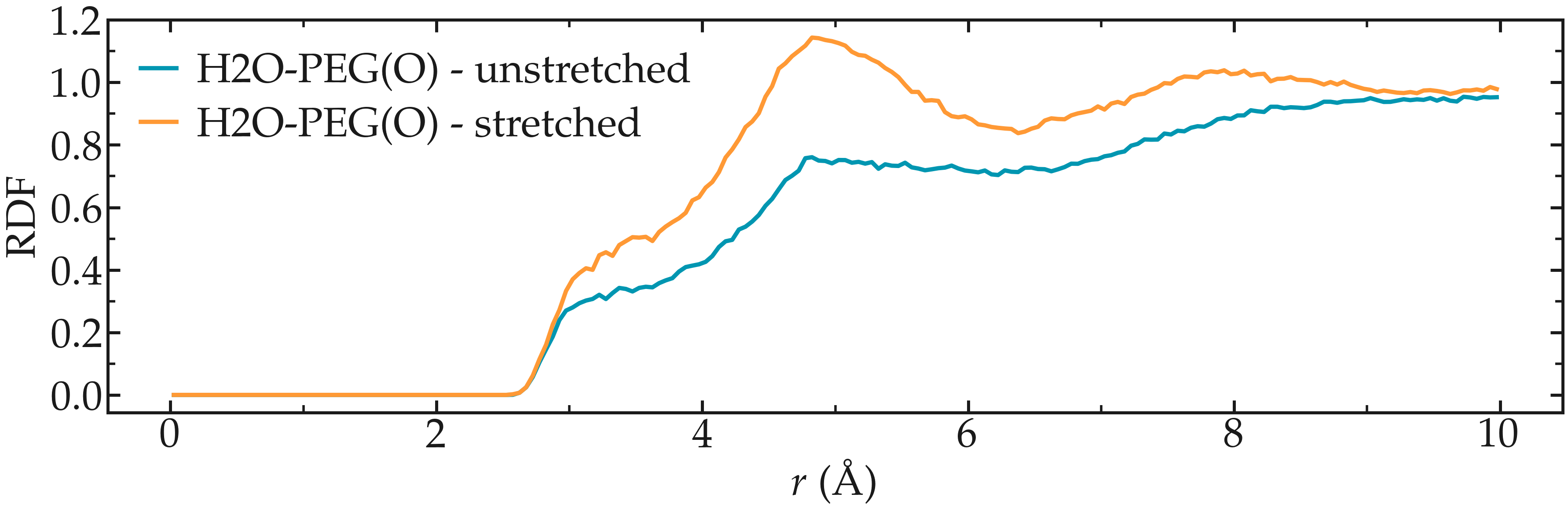
Figure: Radial distribution function between the oxygen atoms of water, as well as between the oxygen atoms of water and the oxygen atoms of the PEG molecule.
Note the difference in the structure of the water before and after the PEG molecule is stretched. This effect is described in the 2017 publication by Liese et al. [27].
Add salt to the system¶
Realistic systems usually contain ions. Let us add some \(\text{Na}^+\) and \(\text{Cl}^-\) ions to our current PEG-water system.
Add some \(\text{Na}^+\) and \(\text{Cl}^-\) ions to the mixture using the method of your choice. \(\text{Na}^+\) ions are characterised by their mass \(m = 22.98\,\text{g/mol}\), their charge \(q = +1\,e\), and Lennard-Jones parameters, \(\epsilon = 0.0469\,\text{kcal/mol}, \sigma = 0.243\,\text{nm}\), and \(\text{Cl}^-\) ions by their mass \(m = 35.453\,\text{g/mol}\), charge \(q = -1\,e\) and Lennard-Jones parameters, \(\epsilon = 0.15\,\text{kcal/mol}, \sigma = 0.4045\,\text{nm}\).
Figure: A PEG molecule in the electrolyte with \(\text{Na}^+\) ions in purple and \(\text{Cl}^-\) ions in cyan.
Evaluate the deformation of the PEG¶
Once the PEG is fully stretched, its structure differs from the unstretched case. The deformation can be probed by extracting the typical intra-molecular parameters, such as the typical angles of the dihedrals.
Extract the histograms of the angular distribution of the PEG dihedrals in the absence and the presence of stretching.
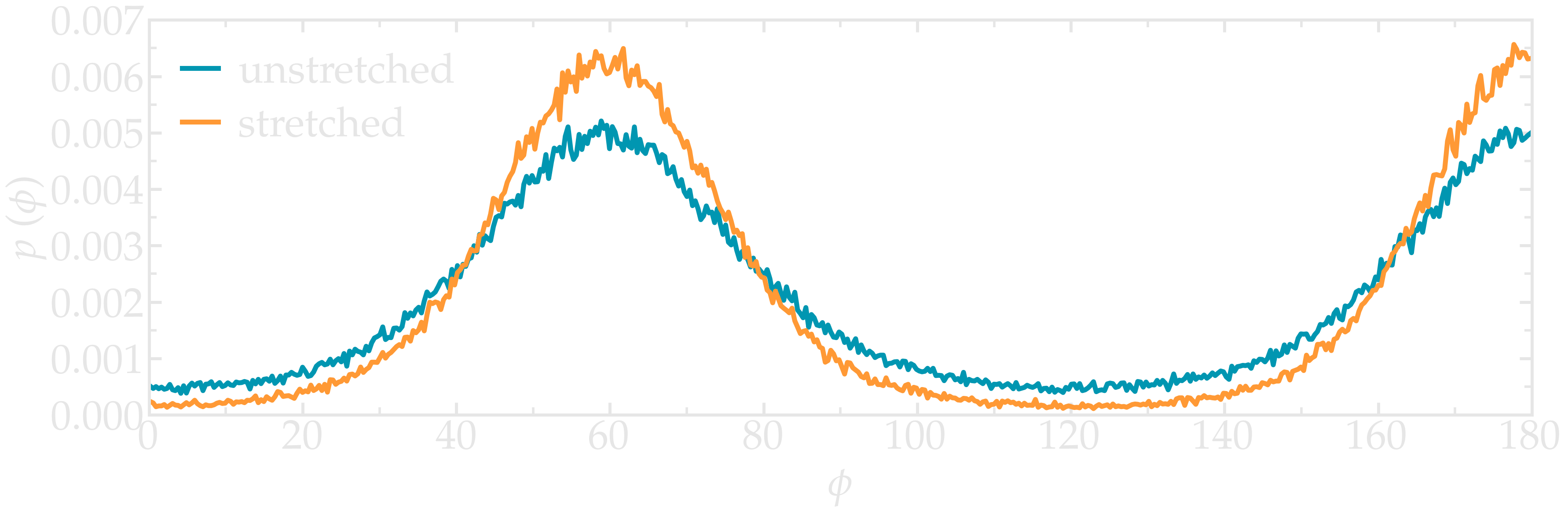
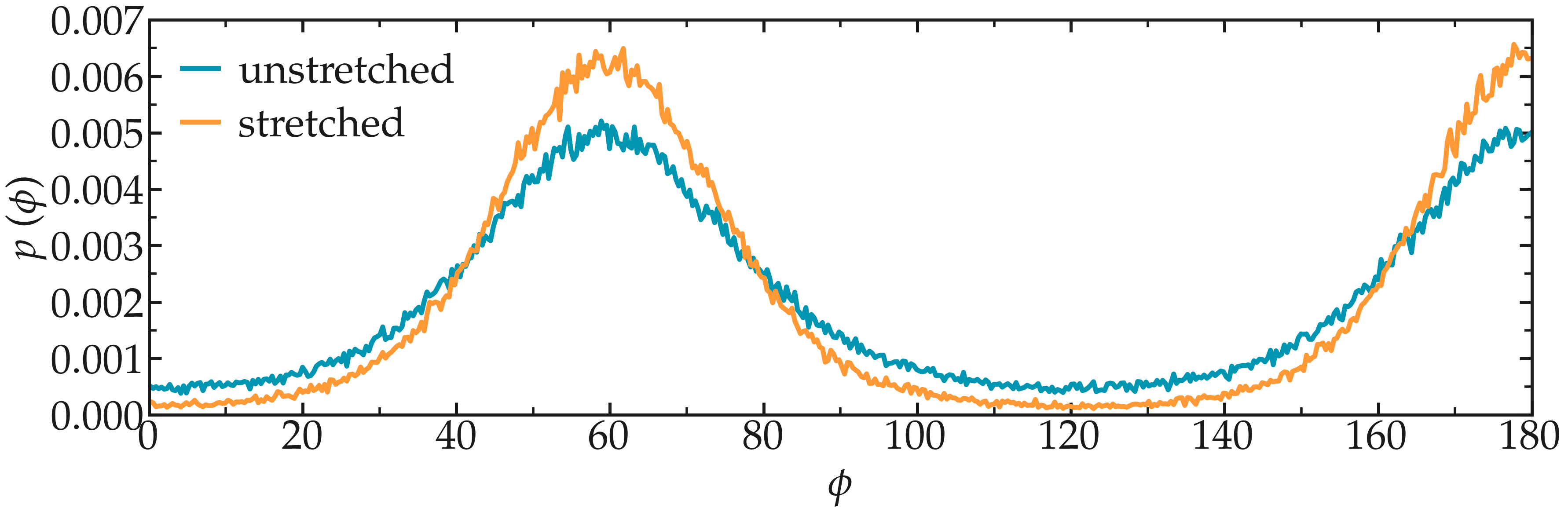
Figure: Probability distribution for the dihedral angle \(\phi\), for a stretched and for an unstretched PEG molecule.