Free energy calculation¶
Sampling a free energy barrier

The objective of this tutorial is to measure a free energy profile of particles across a barrier potential using two methods: free sampling and umbrella sampling [8, 9, 46].
For simplicity and to reduce computation time, the barrier potential will be imposed on the atoms with an additional force, mimicking the presence of a repulsive area in the middle of the simulation box without the need to simulate extra atoms. The procedure is valid for more complex systems and can be adapted to many other situations, such as measuring the adsorption barrier near an interface, or for calculating a translocation barrier through a membrane [47, 48, 49].
If you are completely new to LAMMPS, I recommend that you follow this tutorial on a simple Lennard-Jones fluid first.
Looking for help or have feedback for us?
Visit the Looking for help? page to get in touch with us.
This tutorial is compatible with the 2Aug2023 LAMMPS version.
What is free energy
The free energy refers to the potential energy of a system that is available to perform work. In molecular simulations, it is common to calculate free energy differences between different states or conformations of a molecular system. This can be useful in understanding the thermodynamics of a system, predicting reaction pathways, and determining the stability of different molecular configurations.
Method 1: Free sampling¶
The most direct way to calculate a free energy profile is to extract the partition function from a classic (i.e., unbiased) molecular dynamics simulation, and then estimate the Gibbs free energy using
where \(\Delta G\) is the free energy difference, \(R\) is the gas constant, \(T\) is the temperature, \(p\) is the pressure, and \(p_0\) is a reference pressure. As an illustration, let us apply this method to an extremely simple configuration that consists of a few particles diffusing in a box in the presence of a position-dependent repelling force that makes the center of the box a relatively unfavorable area to explore.
Basic LAMMPS parameters¶
Create a folder named FreeSampling/, and create an input script named input.lammps in it. Copy the following lines into it:
variable sigma equal 3.405 # Angstrom
variable epsilon equal 0.238 # Kcal/mol
variable U0 equal 1.5*${epsilon} # Kcal/mol
variable dlt equal 0.5 # Angstrom
variable x0 equal 5.0 # Angstrom
units real
atom_style atomic
pair_style lj/cut 3.822
pair_modify shift yes
boundary p p p
Here, we start by defining variables for the Lennard-Jones interaction \(\sigma\) and \(\epsilon\) and for the repulsive potential \(U (x)\): \(U_0\), \(\delta\), and \(x_0\), see the analytical expression below. With \(U_0 = 1.5 \epsilon = 0.36\,\text{kcal/mol}\), \(U_0\) is of the same order as the thermal energy \(k_\text{B} T = 0.24,\text{kcal/mol}\), where \(k_\text{B} = 0.002\,\text{kcal/mol/K}\) is the Boltzmann constant and \(T = 119.8\,\text{K}\) (see below). In this case, particles are expected to regularly overcome the energy barrier thanks to the thermal agitation.
The value of 3.822 for the cut-off was chosen to create a WCA, purely repulsive, potential [50]. It was calculated as \(2^{1/6} \times 3.405\) where \(3.405 = \sigma\).
The system of unit real, for which energy is in kcal/mol, distance in Ångstrom, or time in femtosecond, has been chosen for practical reasons: the WHAM algorithm used in the second part of the tutorial automatically assumes the energy to be in kcal/mol. Atoms will interact through a Lennard-Jones potential with a cut-off equal to \(\sigma \times 2 ^ {1/6}\) (i.e. a WCA repulsive potential). The potential is shifted to be equal to 0 at the cut-off using the pair_modify.
System creation and settings¶
Let us define the simulation block and randomly add atoms by adding the following lines into input.lammps:
region myreg block -25 25 -5 5 -25 25
create_box 1 myreg
create_atoms 1 random 60 341341 myreg overlap 1.5 maxtry 50
mass * 39.95
pair_coeff * * ${epsilon} ${sigma}
neigh_modify every 1 delay 4 check yes
The values for the Lennard-Jones parameters (\(\sigma\) and \(\epsilon\)) and the mass (\(m = 39.95\)) are typical of argon.
The variables \(U_0\), \(\delta\), and \(x_0\) defined in the previous subsection are used here to create the repulsive potential, restricting the atoms from exploring the center of the box:
From the derivative of the potential with respect to \(x\), we obtain the expression for the force that will be imposed on the atoms:
The potential and force along the \(x\) axis resembles:
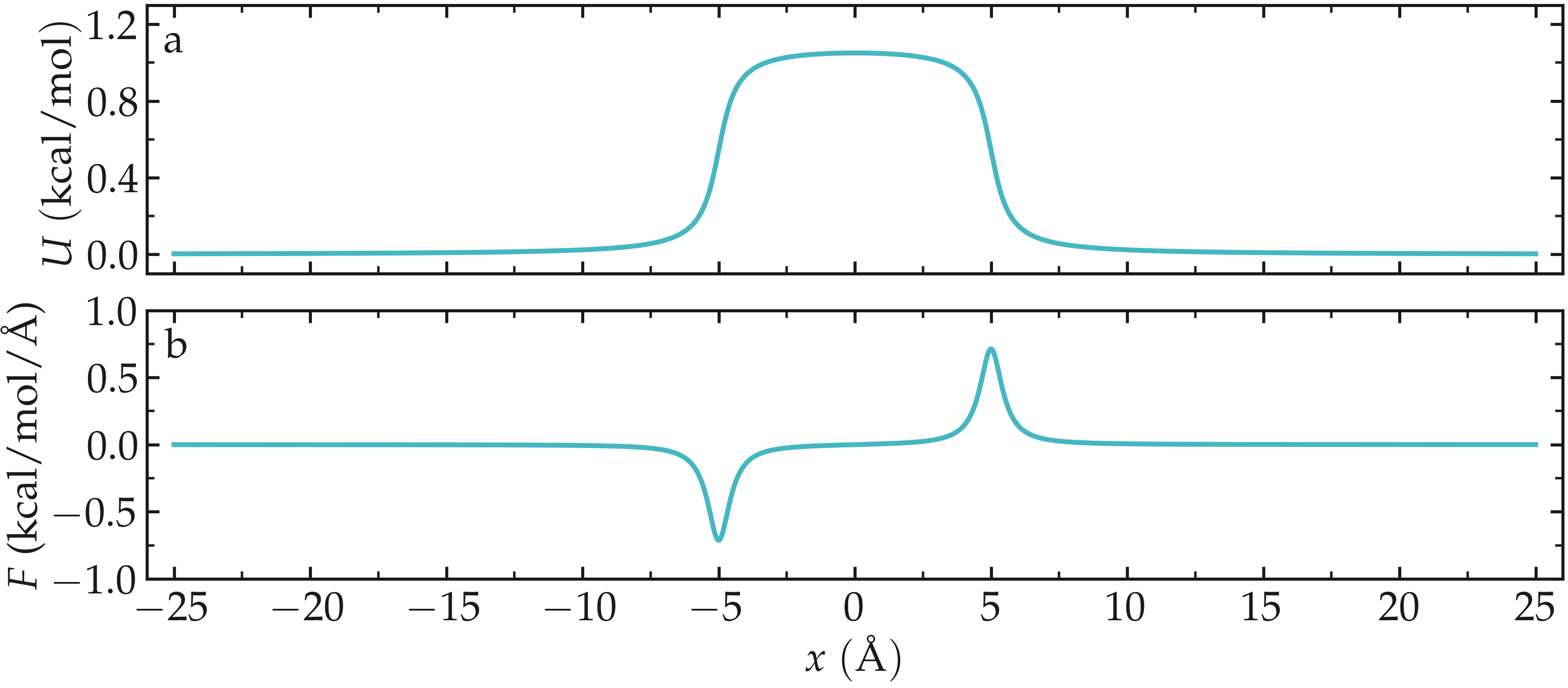
Figure: Potential \(U (x)\) (a) and force \(F (x)\) (b) imposed to the atoms as a function of the coordinate \(x\).
Energy minimization and equilibration
Let us apply energy minimization to the system, and then impose the force \(F(x)\) to all of the atoms in the simulation using the addforce command. Add the following lines to input.lammps:
minimize 1e-4 1e-6 100 1000
reset_timestep 0
variable U atom ${U0}*atan((x+${x0})/${dlt}) &
-${U0}*atan((x-${x0})/${dlt})
variable F atom ${U0}/((x-${x0})^2/${dlt}^2+1)/${dlt} &
-${U0}/((x+${x0})^2/${dlt}^2+1)/${dlt}
fix myadf all addforce v_F 0.0 0.0 energy v_U
Finally, let us combine the fix nve with a Langevin thermostat and run a molecular dynamics simulation. With these two commands, the MD simulation is effectively in the NVT ensemble: constant number of atoms \(N\), constant volume \(V\), and constant temperature \(T\). Let us perform an equilibration of 500000 steps in total, using a timestep of \(2\,\text{fs}\) (i.e. a total duration of \(1\,\text{ns}\)).
To make sure that \(1\,\text{ns}\) is long enough, we will record the evolution of the number of atoms in the central (energetically unfavorable) region called mymes:
fix mynve all nve
fix mylgv all langevin 119.8 119.8 50 1530917
region mymes block -${x0} ${x0} INF INF INF INF
variable n_center equal count(all,mymes)
fix myat all ave/time 10 50 500 v_n_center file density_evolution.dat
timestep 2.0
thermo 10000
run 500000
Run and data acquisition¶
Finally, let us record the density profile of the atoms along the \(x\) axis using the ave/chunk command. A total of 10 density profiles will be printed. The step count is reset to 0 to synchronize with the output times of fix density/number, and the fix myat is canceled (it has to be canceled before a reset time):
unfix myat
reset_timestep 0
compute cc1 all chunk/atom bin/1d x 0.0 1.0
fix myac all ave/chunk 10 400000 4000000 &
cc1 density/number &
file density_profile.dat
dump mydmp all atom 200000 dump.lammpstrj
thermo 100000
run 4000000
This simulation with a total duration of \(9\,\text{ns}\) needs a few minutes to complete. Feel free to increase the duration of the last run for smoother results.

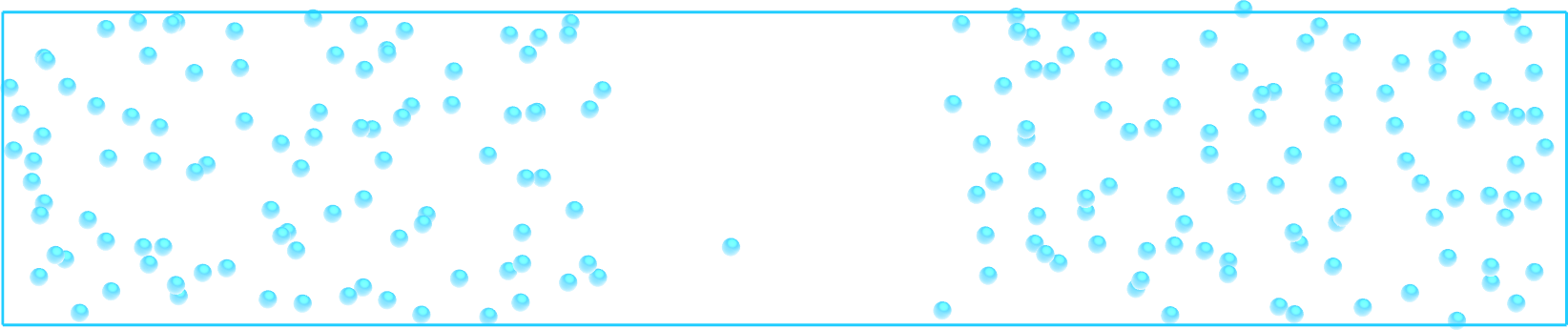
Figure: Snapshot of the system. Notice that the density of atoms is lower in the central part of the box, due to the additional force \(F (x)\).
Data analysis¶
First, let us ensure that the initial equilibration of \(1\,\text{ns}\) is long enough by examining the density_evolution.dat file.
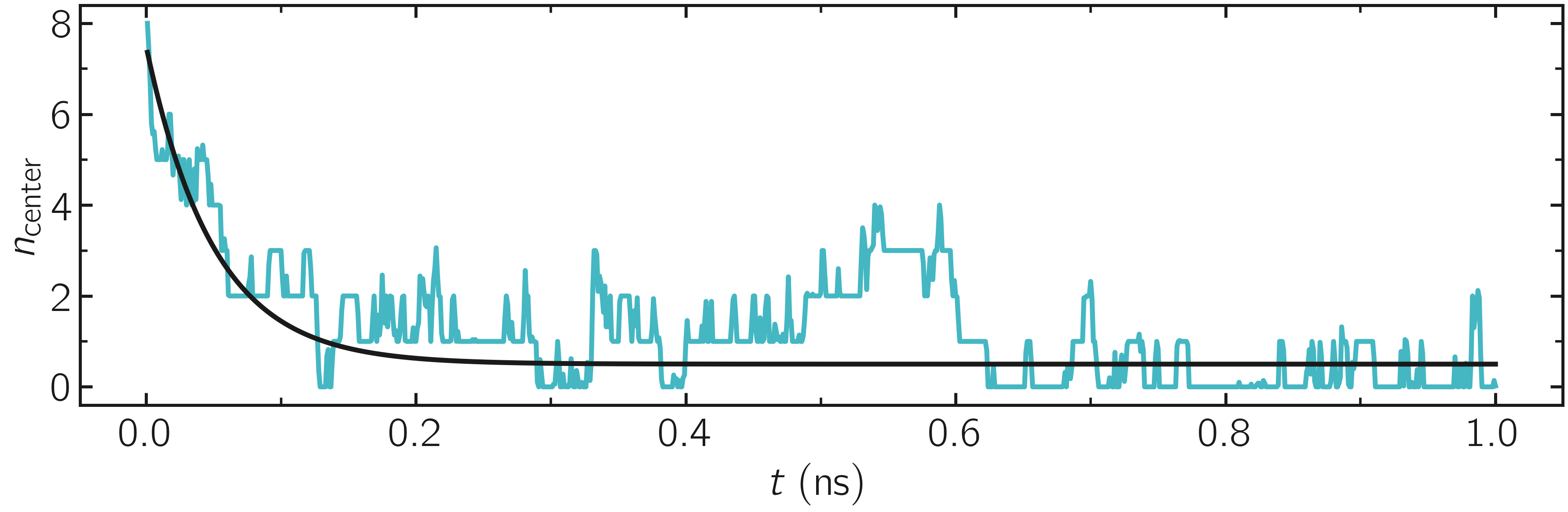
Figure: Evolution of the number of atoms in the central region during equilibration.
Here, we can see that the number of atoms in the central region, \(n_\mathrm{central}\), evolves near its equilibrium value (which is close to 0) after about \(0.1\,\text{ns}\).
One can also look at the density profile, which shows that the density in the center of the box is about two orders of magnitude lower than inside the reservoir.
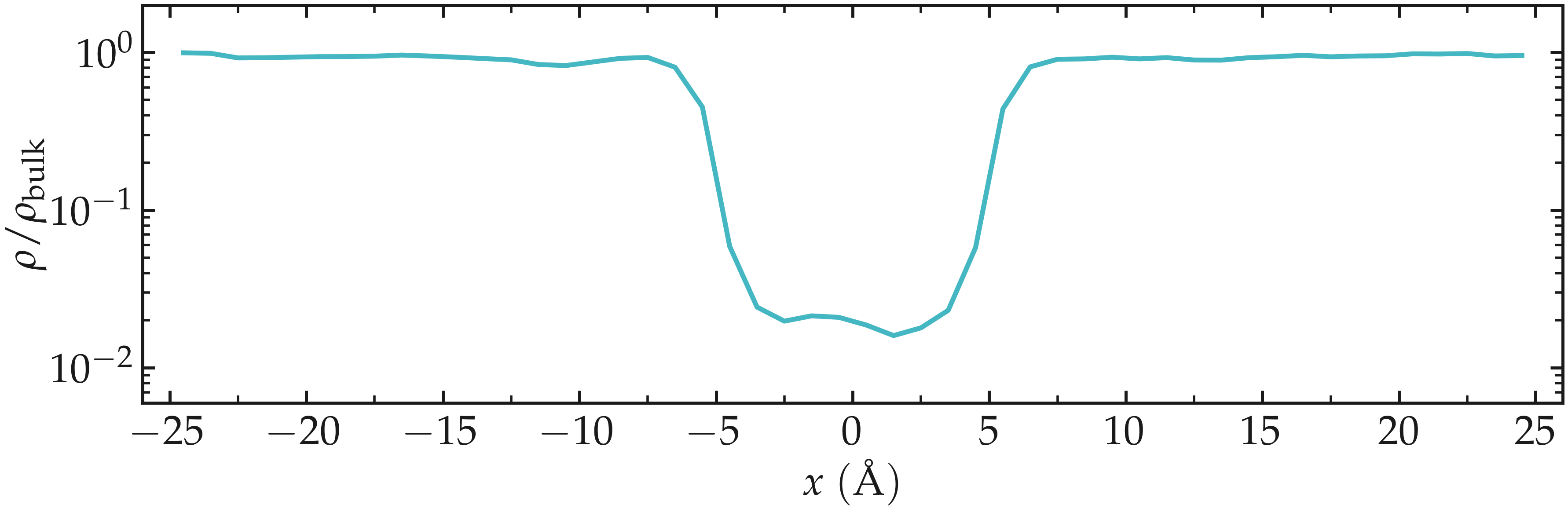
Figure: Fluid density \(\rho\) along the \(x\) direction in the presence of a repulsive potential with \(U_0 = 1.5 \epsilon\). The reference density is \(\rho_\text{bulk} = 0.0033~\text{Å}^{-3}\).
Then, let us plot \(-R T \ln(\rho/\rho_\mathrm{bulk})\) and compare it with the imposed (reference) potential \(U\).
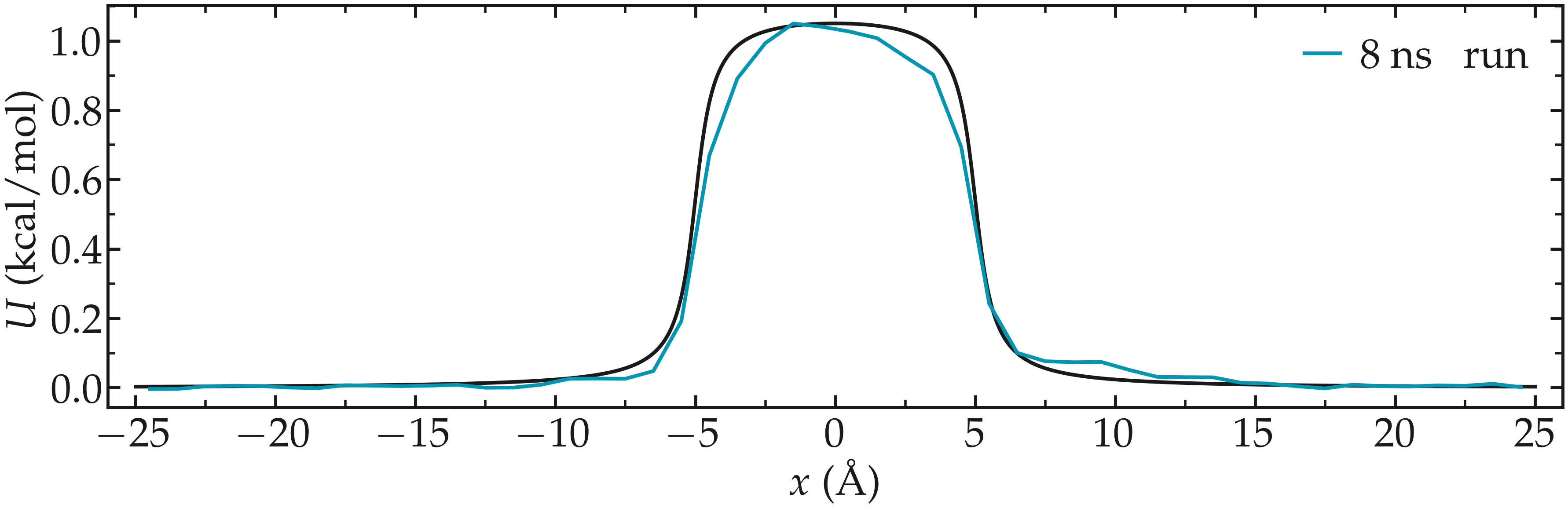
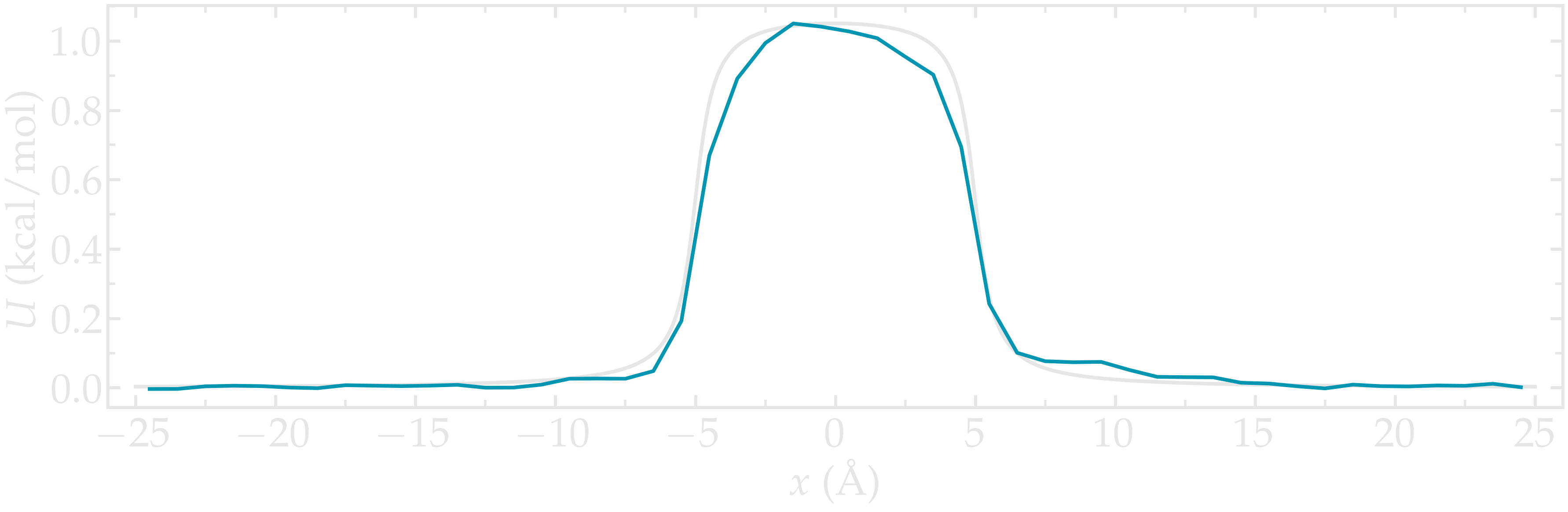
Figure: Calculated potential \(-R T \ln(\rho/\rho_\mathrm{bulk})\) compared to the imposed potential with \(U_0 = 1.5 \epsilon\). The calculated potential is in blue.
The agreement with the expected energy profile is reasonable, despite some noise in the central part (where fewer data points are available due to the repulsive potential).
The limits of free sampling¶
If we increase the value of \(U_0\), the average number of atoms in the central region will decrease, making it difficult to obtain a good resolution for the free energy profile. For instance, when we run the same simulation using \(U_0 = 10 \epsilon\), which corresponds to a situation where \(U_0 \approx 10 k_\text{B} T\), not a single atom explores the central part of the simulation box during the 8 ns of simulation. In this case, using an enhanced sampling method is preferred; see the next section.
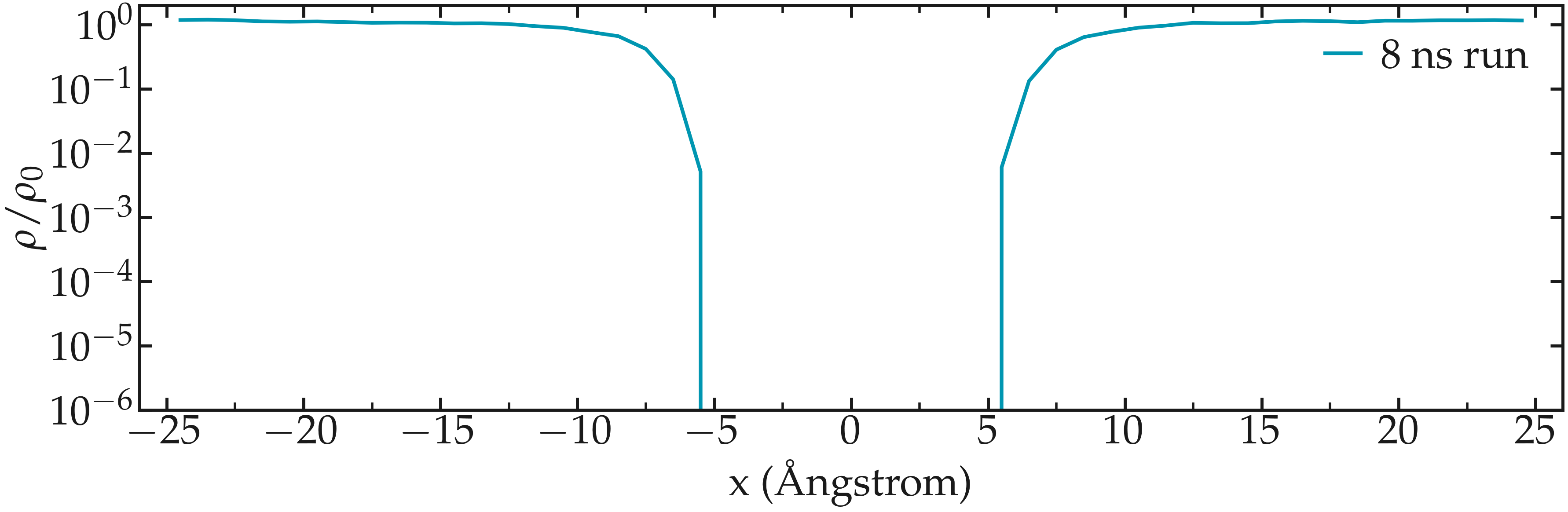
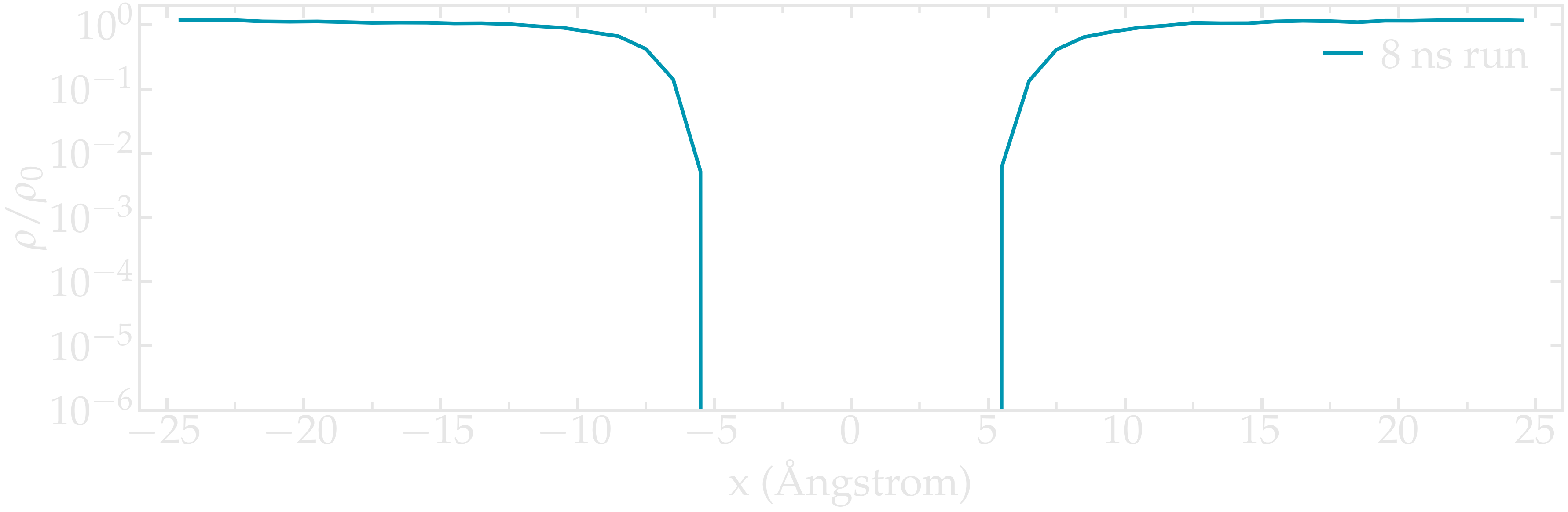
Figure: Fluid density \(\rho\) along the \(x\) direction in the presence of a repulsive potential with \(U_0 = 10 \epsilon\).
In that case, it is better to use the umbrella sampling method to extract free energy profiles, see the next section.
Method 2: Umbrella sampling¶
Umbrella sampling is a biased molecular dynamics method in which additional forces are added to a chosen atom to force it to explore the entire space, including the more unfavorable areas of the system [8, 9, 46].
To encourage one of the atoms to explore the central region of the box, we apply a potential \(V\) and force it to move along the \(x\)-axis. The chosen path is called the axis of reaction. Several simulations (or windows) will be conducted with varying parameters for the applied biasing. The results will be analyzed using the weighted histogram analysis method (WHAM) [51], which allows for the removal of the biasing effect and ultimately deduces the unbiased free energy profile.
LAMMPS input script¶
Create a new folder called BiasedSampling/, and create a new input file named input.lammps in it. Copy the following lines into input.lammps:
variable sigma equal 3.405 # Angstrom
variable epsilon equal 0.238 # Kcal/mol
variable U0 equal 10*${epsilon} # Kcal/mol
variable dlt equal 0.5 # Angstrom
variable x0 equal 5.0 # Angstrom
variable k equal 1.5 # Kcal/mol/Angstrom^2
units real
atom_style atomic
pair_style lj/cut 3.822 # 2^(1/6) * 3.405 WCA potential
pair_modify shift yes
boundary p p p
region myreg block -25 25 -5 5 -25 25
create_box 2 myreg
create_atoms 2 single 0 0 0
create_atoms 1 random 59 341341 myreg overlap 1.5 maxtry 50
mass * 39.948
pair_coeff * * ${epsilon} ${sigma}
neigh_modify every 1 delay 4 check yes
group topull type 2
minimize 1e-4 1e-6 100 1000
reset_timestep 0
variable U atom ${U0}*atan((x+${x0})/${dlt}) &
-${U0}*atan((x-${x0})/${dlt})
variable F atom ${U0}/((x-${x0})^2/${dlt}^2+1)/${dlt} &
-${U0}/((x+${x0})^2/${dlt}^2+1)/${dlt}
fix pot all addforce v_F 0.0 0.0 energy v_U
fix mynve all nve
fix mylgv all langevin 119.8 119.8 50 1530917
timestep 2.0
thermo 100000
run 500000
reset_timestep 0
dump mydmp all atom 1000000 dump.lammpstrj
So far, this code resembles that of Method 1, except for the additional particle of type 2. Particles of type 1 and 2 are identical, having the same mass and Lennard-Jones parameters. However, the particle of type 2 will additionally be exposed to the biasing potential \(V\).
Let us create a loop with 50 steps, and move progressively the center of the bias potential by an increment of 0.1 nm. Add the following lines to input.lammps:
variable a loop 50
label loop
variable xdes equal ${a}-25
variable xave equal xcm(topull,x)
fix mytth topull spring tether ${k} ${xdes} 0 0 0
run 200000
fix myat1 all ave/time 10 10 100 v_xave v_xdes &
file data-k1.5/position.${a}.dat
run 1000000
unfix myat1
next a
jump SELF loop
A folder named data-k1.5/ needs to be created within BiasedSampling/.
The spring command serves to impose the additional harmonic potential with the spring constant \(k\). Note that the value of \(k\) should be chosen with care, if \(k\) is too small, the particle won’t follow the biasing potential center, if \(k\) is too large, there will be no overlapping between the different windows. See the side note named on the choice of k below.
The center of the harmonic potential \(x_\text{des}\) successively takes values from -25 to 25. For each value of \(x_\text{des}\), an equilibration step of 0.4 ns is performed, followed by a step of 2 ns during which the position along \(x\) of the particle is saved in data files (one data file per value of \(x_\text{des}\)). You can always increase the duration of the runs for better samplings.
WHAM algorithm¶
To generate the free energy profile from the density distribution, let us use the WHAM algorithm as implemented by Alan Grossfield [52].
You can download it from Alan Grossfield website, and compile it using:
cd wham
make clean
make
The compilation creates an executable called wham that you can copy in the BiasedSampling/ folder. Alternatively, use the version 2.0.11 I have downloaded, or try your luck with the version I precompiled: precompiled wham.
In order to apply the WHAM algorithm to our simulation, we first need to create a metadata file. This file simply contains
the paths to all the data files,
the value of \(x_\text{des}\),
and the values of \(k\).
To generate the metadata.txt file, you can run this Python script from the BiasedSampling/ folder:
import os
k=1.5
folder='data-k1.5/'
f = open("metadata.dat", "w")
for n in range(-50,50):
datafile=folder+'position.'+str(n)+'.dat'
if os.path.exists(datafile):
# read the imposed position is the expected one
with open(datafile) as g:
_ = g.readline()
_ = g.readline()
firstline = g.readline()
imposed_position = firstline.split(' ')[-1][:-1]
# write one file per file
f.write(datafile+' '+str(imposed_position)+' '+str(k)+'\n')
f.close()
Here, \(k\) is in kcal/mol. The generated file named metadata.dat looks like this:
./data-k1.5/position.1.dat -24 1.5
./data-k1.5/position.2.dat -23 1.5
./data-k1.5/position.3.dat -22 1.5
(...)
./data-k1.5/position.48.dat 23 1.5
./data-k1.5/position.49.dat 24 1.5
./data-k1.5/position.50.dat 25 1.5
Alternatively, you can download this metadata.dat file. Then, simply run the following command in the terminal:
./wham -25 25 50 1e-8 119.8 0 metadata.dat PMF.dat
where -25 and 25 are the boundaries, 50 is the number of bins, 1e-8 the tolerance, and 119.8 the temperature. A file named PMF.dat has been created and contains the free energy profile in Kcal/mol.
Results
Again, one can compare the result of the PMF with the imposed potential \(U\), which shows that the agreement is excellent.
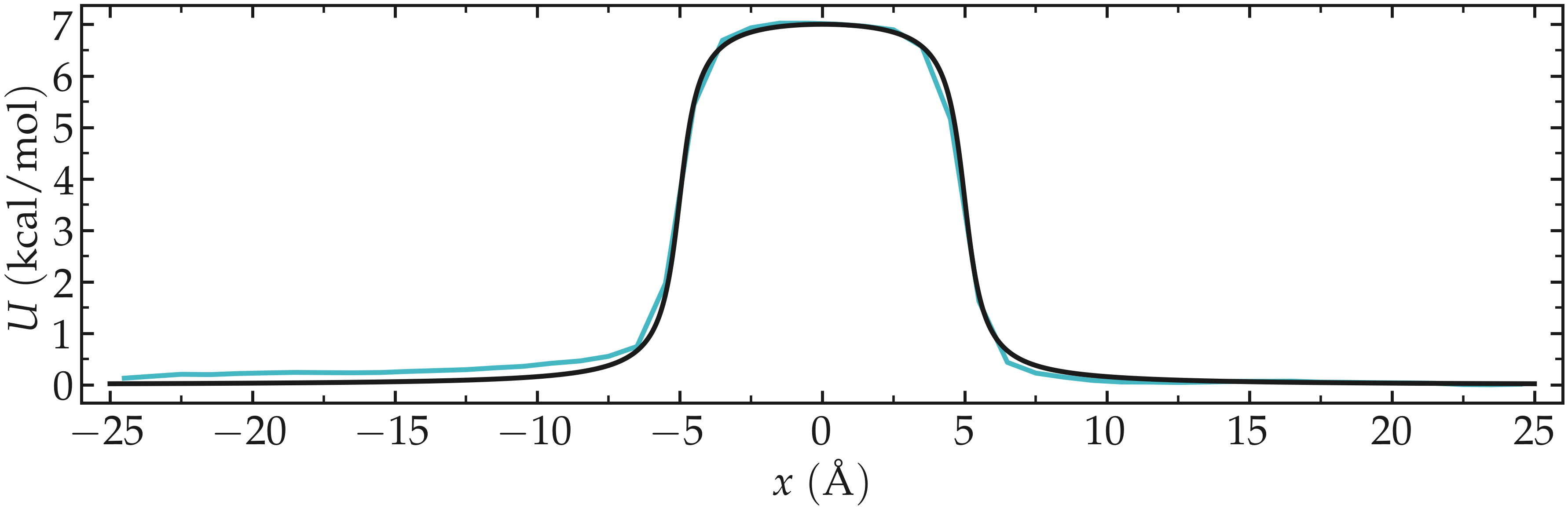
Figure: Calculated potential using umbrella sampling compared to the imposed potential with \(U_0 = 10 \epsilon\). The calculated potential is in blue.
We can see that the agreement is quite good despite the very short calculation time and the very high value for the energy barrier. Obtaining the same results with Free Sampling would require performing extremely long and costly simulations.
You can access the input scripts and data files that are used in these tutorials from this Github repository. This repository also contains the full solutions to the exercises.
Side note: on the choice of k¶
As already stated, one difficult part of umbrella sampling is to choose the value of \(k\). Ideally, you want the biasing potential to be strong enough to force the chosen atom to move along the axis, and you also want the fluctuations of the atom position to be large enough to have some overlap in the density probability of two neighbor positions. Here, 3 different values of \(k\) are being tested.
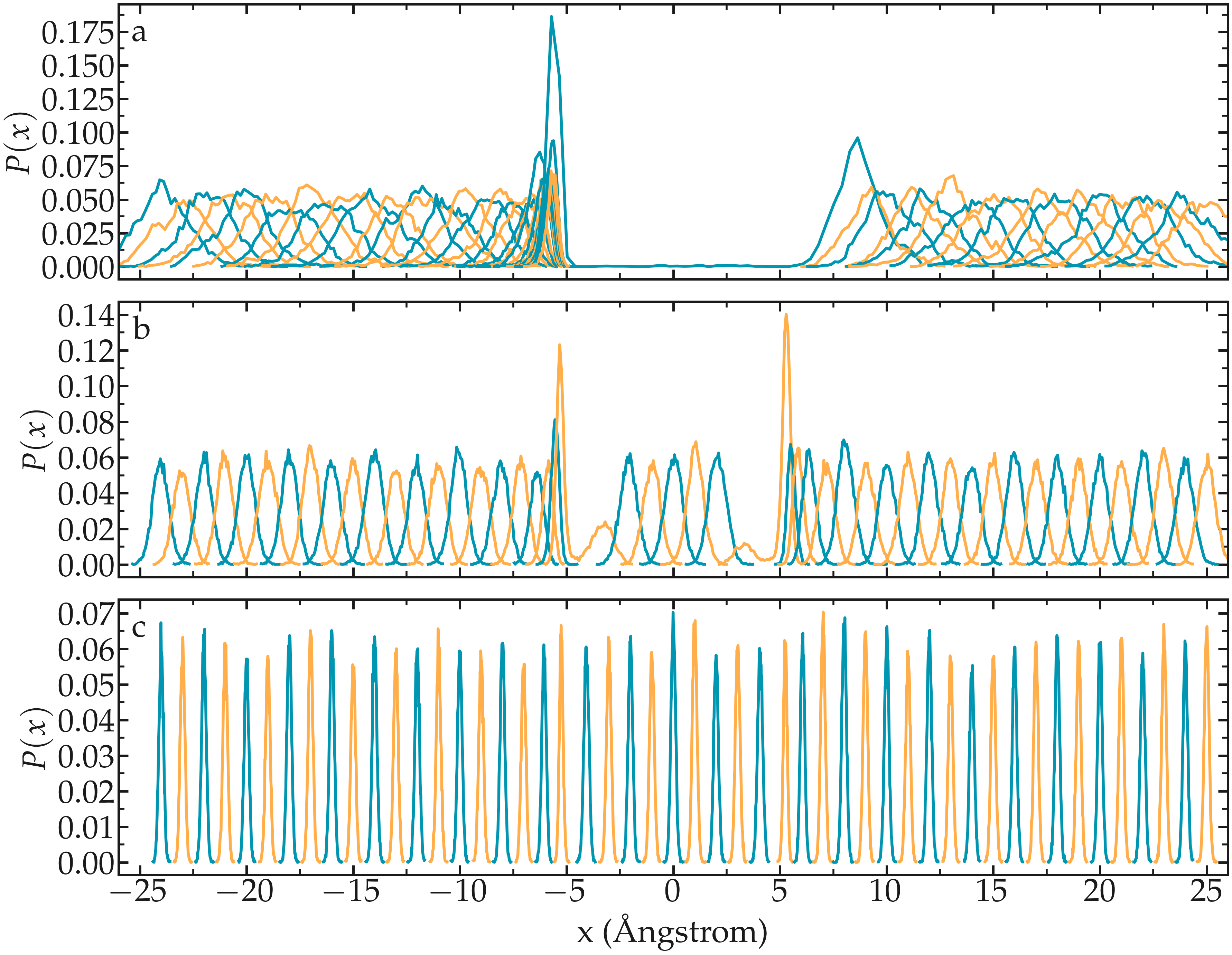
Figure: Density probability for each run with \(k = 0.15\,\text{Kcal}/\text{mol}/Å^2\) (a), \(k = 1.5\,\text{Kcal}/\text{mol}/Å^2\) (b), and \(k = 15\,\text{Kcal}/\text{mol}/Å^2\) (c).
If \(k\) is too small, the biasing potential is too weak to force the particle to explore the region of interest, making it impossible to reconstruct the PMF.
If \(k\) is too large, the biasing potential is too large compared to the potential one wants to probe, which reduces the sensitivity of the method.
Going further with exercises¶
Each exercise comes with a proposed solution, see Solutions to the exercises.
The binary fluid that won’t mix¶
1 - Create the system
Create a molecular simulation with two species of respective types 1 and 2. Apply different potentials \(U1\) and \(U2\) on particles of types 1 and 2, respectively, so that particles of type 1 are excluded from the center of the box, while at the same time particles of type 2 are excluded from the rest of the box.

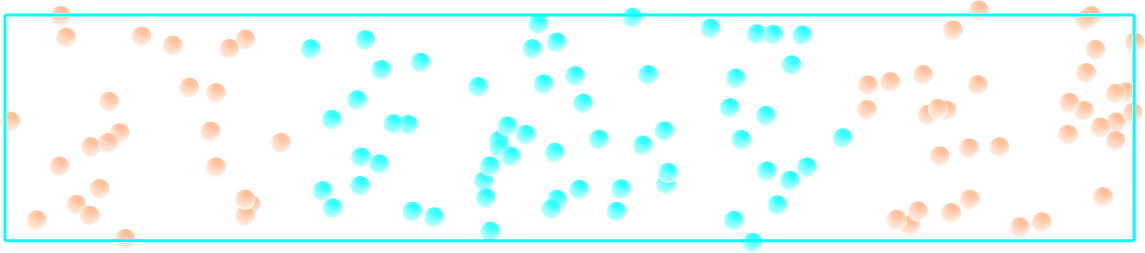
Figure: Particles of type 1 and 2 separated by two different potentials.
2 - Measure the PMFs
Using the same protocol as the one used in the tutorial (i.e. umbrella sampling with the wham algorithm), extract the PMF for each particle type.
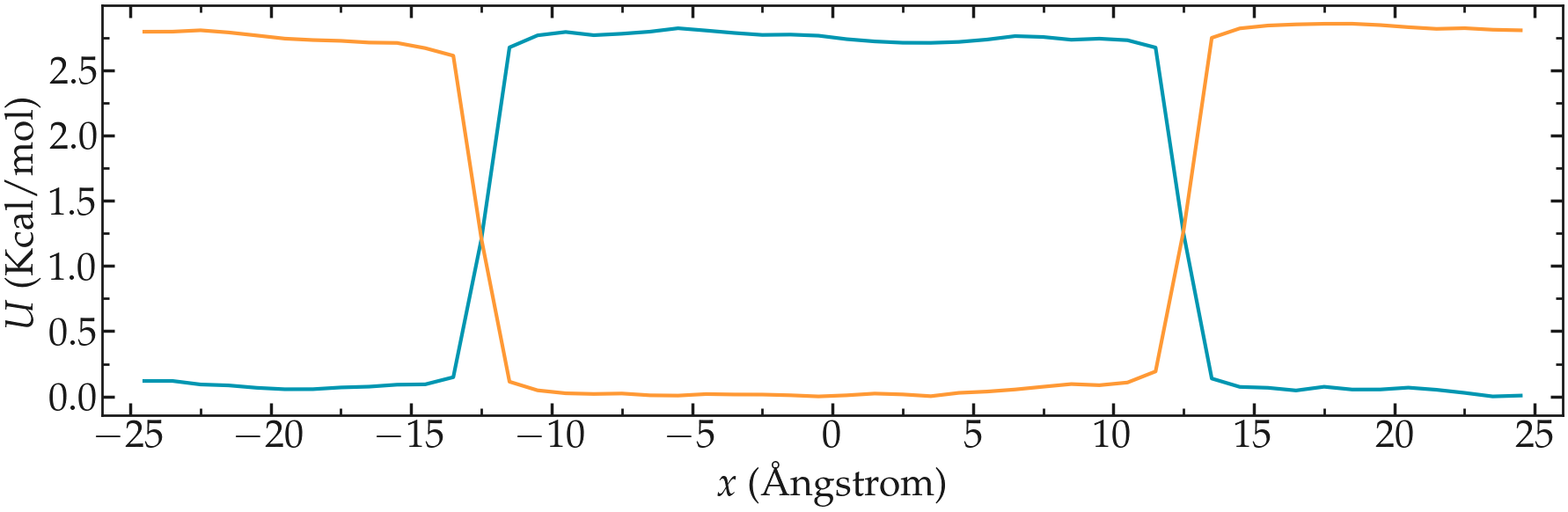
Figure: PMFs calculated for both atom types.
Particles under convection¶
Use a similar simulation as the one from the tutorial, with a repulsive potential in the center of the box. Add force to the particles and force them to flow in the \(x\) direction.
Re-measure the potential in the presence of the flow, and observe the difference with the reference case in the absence of flow.
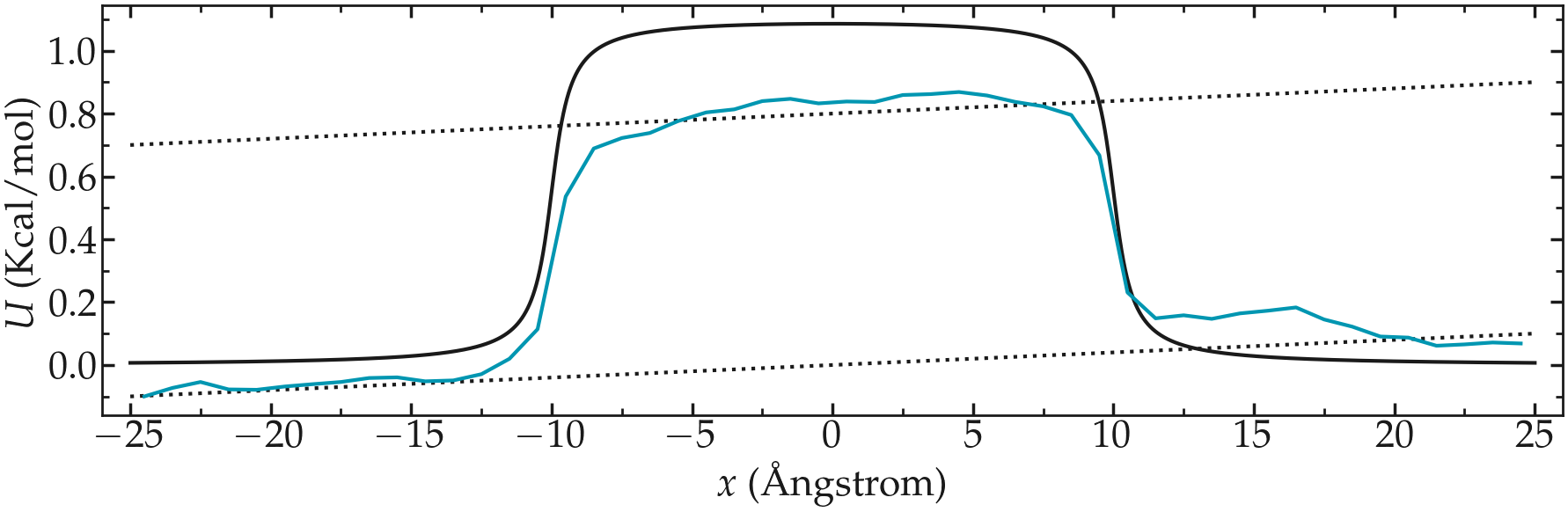
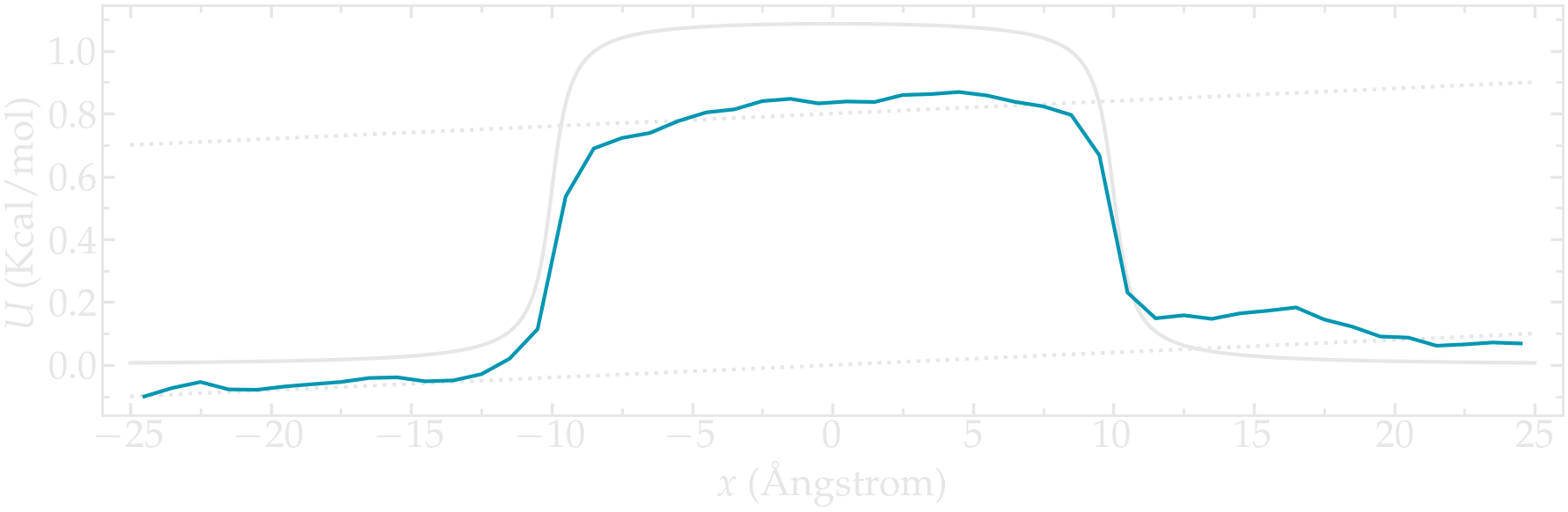
Figure: PMF calculated in the presence of a net force that is inducing the convection of the particles from left to right.
Surface adsorption of a molecule¶
Apply umbrella sampling to calculate the free energy profile of ethanol in the direction normal to a crystal solid surface (here made of sodium chloride). Find the topology files and parameter file.
Use the following lines for starting the input.lammps:
units real # style of units (A, fs, Kcal/mol)
atom_style full # molecular + charge
bond_style harmonic
angle_style harmonic
dihedral_style harmonic
boundary p p p # periodic boundary conditions
pair_style lj/cut/coul/long 10 # cut-off 1 nm
kspace_style pppm 1.0e-4
pair_modify mix arithmetic tail yes
The PMF normal to a solid wall serves to indicate the free energy of adsorption, which can be calculated from the difference between the PMF far from the surface, and the PMF at the wall.
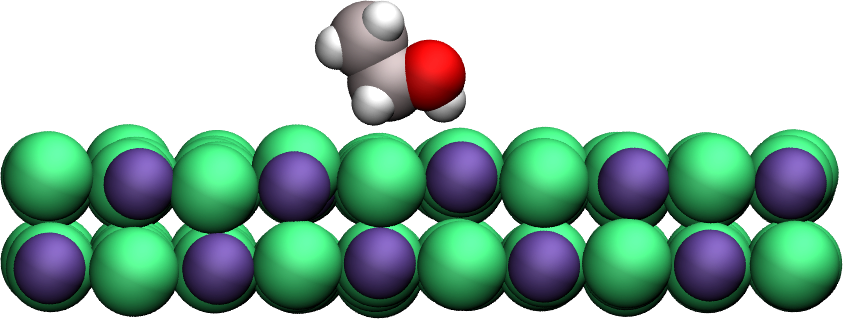
Figure: A single ethanol molecule next to a crystal NaCl(100) wall.
The PMF shows a minimum near the solid surface, which indicates a good affinity between the wall and the molecule.
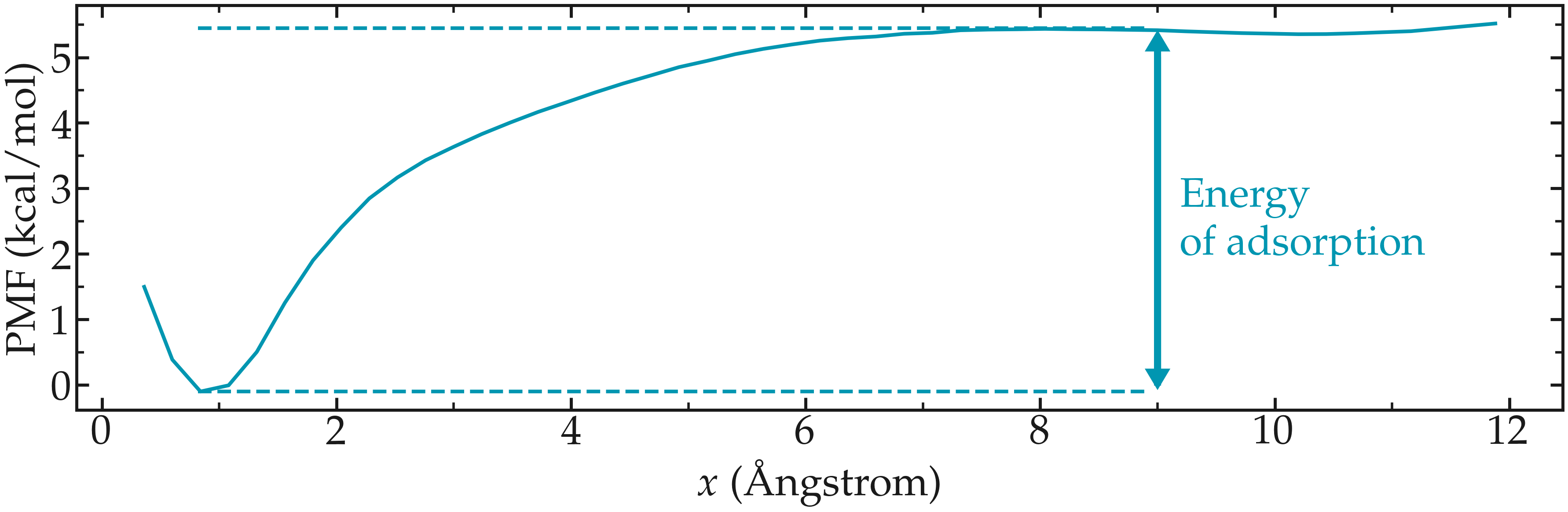
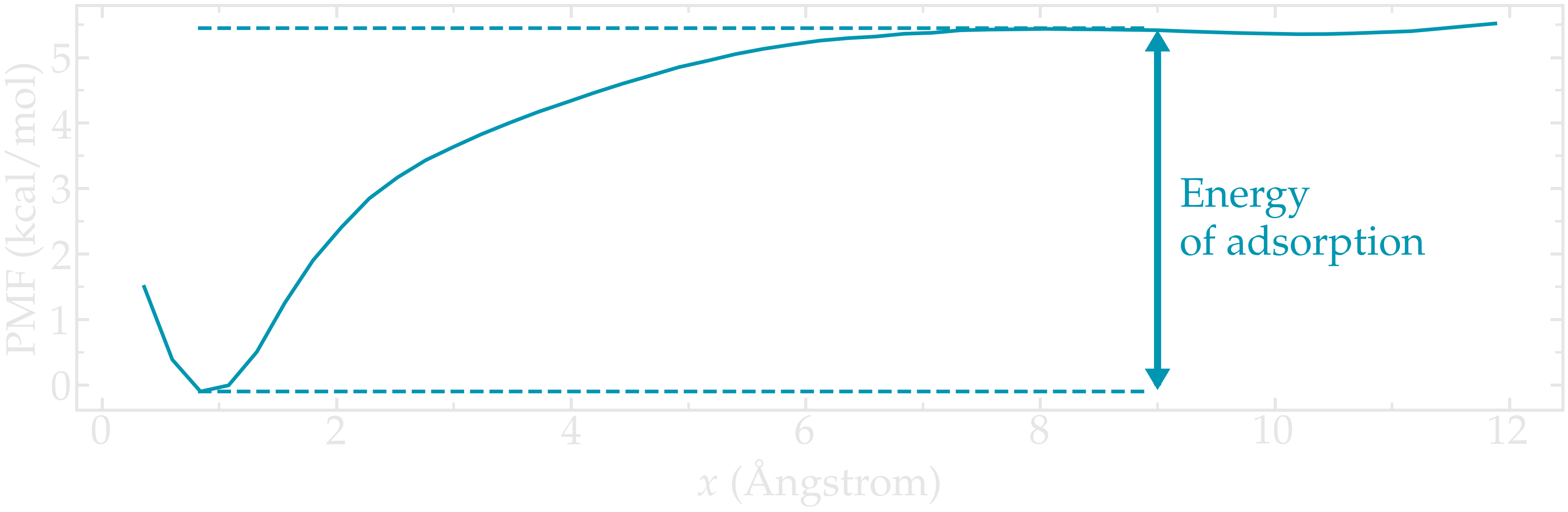
Figure: PMF for a single ethanol molecule next to a NaCl solid surface. The position of the wall is in \(x=0\). The arrow highlights the difference between the energy of the molecule when adsorbed to the solid surface, and the energy far from the surface. This difference corresponds to the free energy of adsorption.
Alternatively to using ethanol, feel free to download the molecule of your choice, for instance from the Automated Topology Builder (ATB). Make your life simpler by choosing a small molecule like CO2.