What is free energy
The free energy refers to the potential energy of a system that is available to perform work. In molecular simulations, it is common to calculate free energy differences between different states or conformations of a molecular system. This can be useful in understanding the thermodynamics of a system, predicting reaction pathways, and determining the stability of different molecular configurations.
Method 1: Free sampling¶
The most direct way to calculate a free energy profile is to extract the partition function from a classical (i.e. unbiased) molecular dynamics simulation, and then estimate the Gibbs free energy by using
where \(\Delta G\) is the free energy difference, \(R\) is the gas constant, \(T\) is the temperature, \(p\) is the pressure, and \(p_0\) is a reference pressure. As an illustration, let us apply this method to a simple configuration that consists of a particles in a box in the presence of a position-dependent repulsive force that makes the center of the box a less favorable area to explore.
Struggling with your molecular simulations project?
Get guidance for your LAMMPS simulations and receive personalized advice for your project.
Basic LAMMPS parameters¶
To begin this tutorial, if you are using LAMMPS–GUI, select Start Tutorial 7
from the Tutorials menu and follow the instructions. Alternatively, if you are
not using LAMMPS–GUI, create a new folder and add a file named
free-sampling.lmp. Open the file in a text editor and paste in the following
content:
variable sigma equal 3.405
variable epsilon equal 0.238
variable U0 equal 1.5*${epsilon}
variable dlt equal 1.0
variable x0 equal 10.0
units real
atom_style atomic
pair_style lj/cut 3.822
pair_modify shift yes
boundary p p p
Here, we begin by defining variables for the Lennard-Jones interaction
\(\sigma\) and \(\epsilon\) and for the repulsive potential
\(U\), which are \(U_0\), \(\delta\), and
\(x_0\) [see Eqs. (2)-(3) below]. The cut-off value of
3.822 Å was chosen to create a Weeks-Chandler-Andersen (WCA) potential,
which is a truncated and purely repulsive LJ
potential [51]. It was calculated as \(2^{1/6} \sigma\).
The potential is also shifted to be equal to 0 at the cut-off
using the pair_modify command.
System creation and settings¶
Let us define the simulation box and randomly add atoms by addying the following lines to free-sampling.lmp:
region myreg block -50 50 -15 15 -50 50
create_box 1 myreg
create_atoms 1 random 200 34134 myreg overlap 3 maxtry 50
mass * 39.95
pair_coeff * * ${epsilon} ${sigma}
The variables \(U_0\), \(\delta\), and \(x_0\), defined in the previous subsection, are used here to create the repulsive potential, restricting the atoms from exploring the center of the box:
Taking the derivative of the potential with respect to \(x\), we obtain the expression for the force that will be imposed on the atoms:
The figure below shows the potential \(U\) and force \(F\) along the \(x\)-axis. With \(U_0 = 1.5 \epsilon = 0.36\,\text{kcal/mol},\) \(U_0\) is of the same order of magnitude as the thermal energy \(k_\text{B} T = 0.24\,\text{kcal/mol}\), where \(k_\text{B} = 0.002\,\text{kcal/mol/K}\) is the Boltzmann constant and \(T = 119.8\,\text{K}\) is the temperature used in this simulation. Under these conditions, particles are expected to frequently overcome the energy barrier due to thermal agitation.
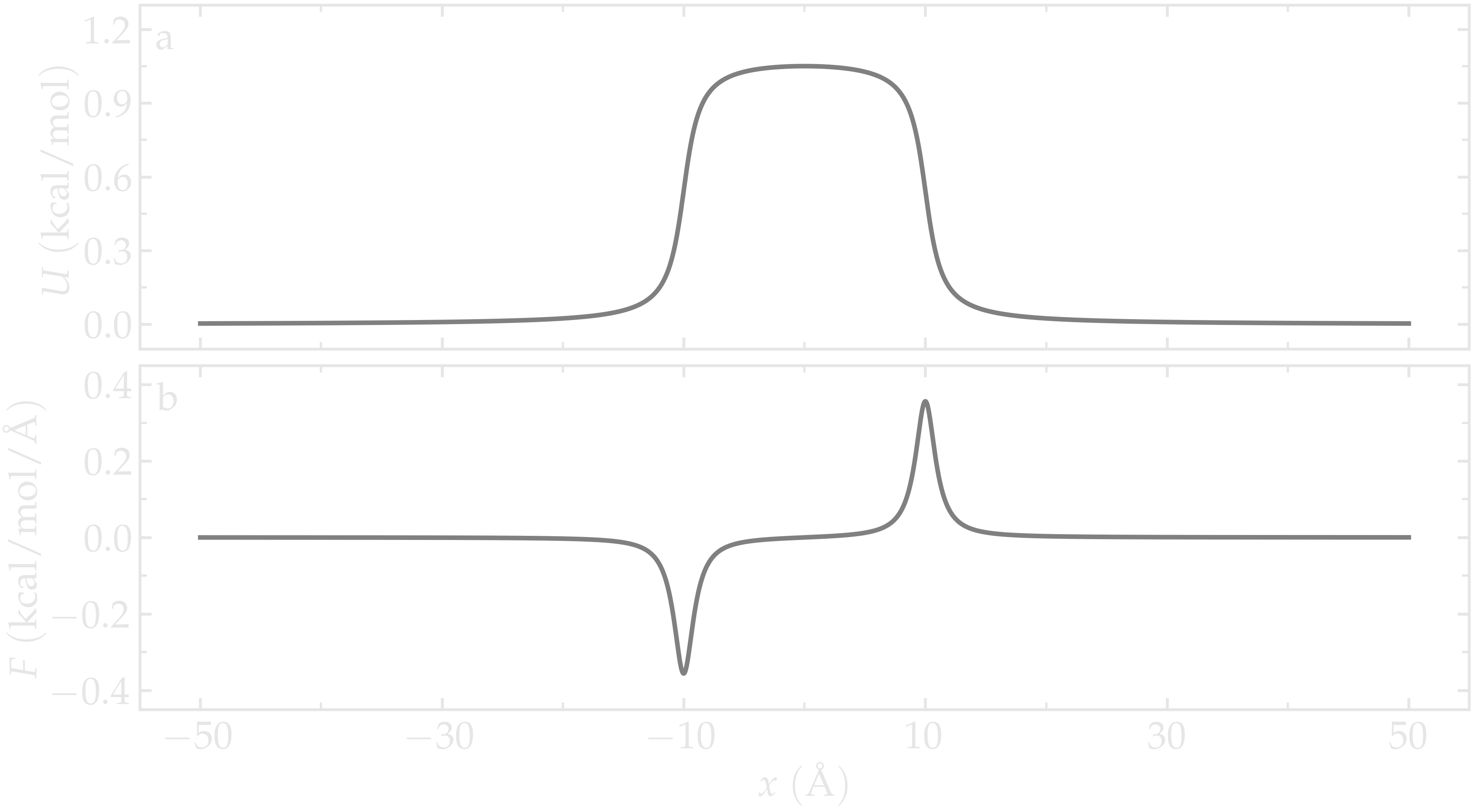
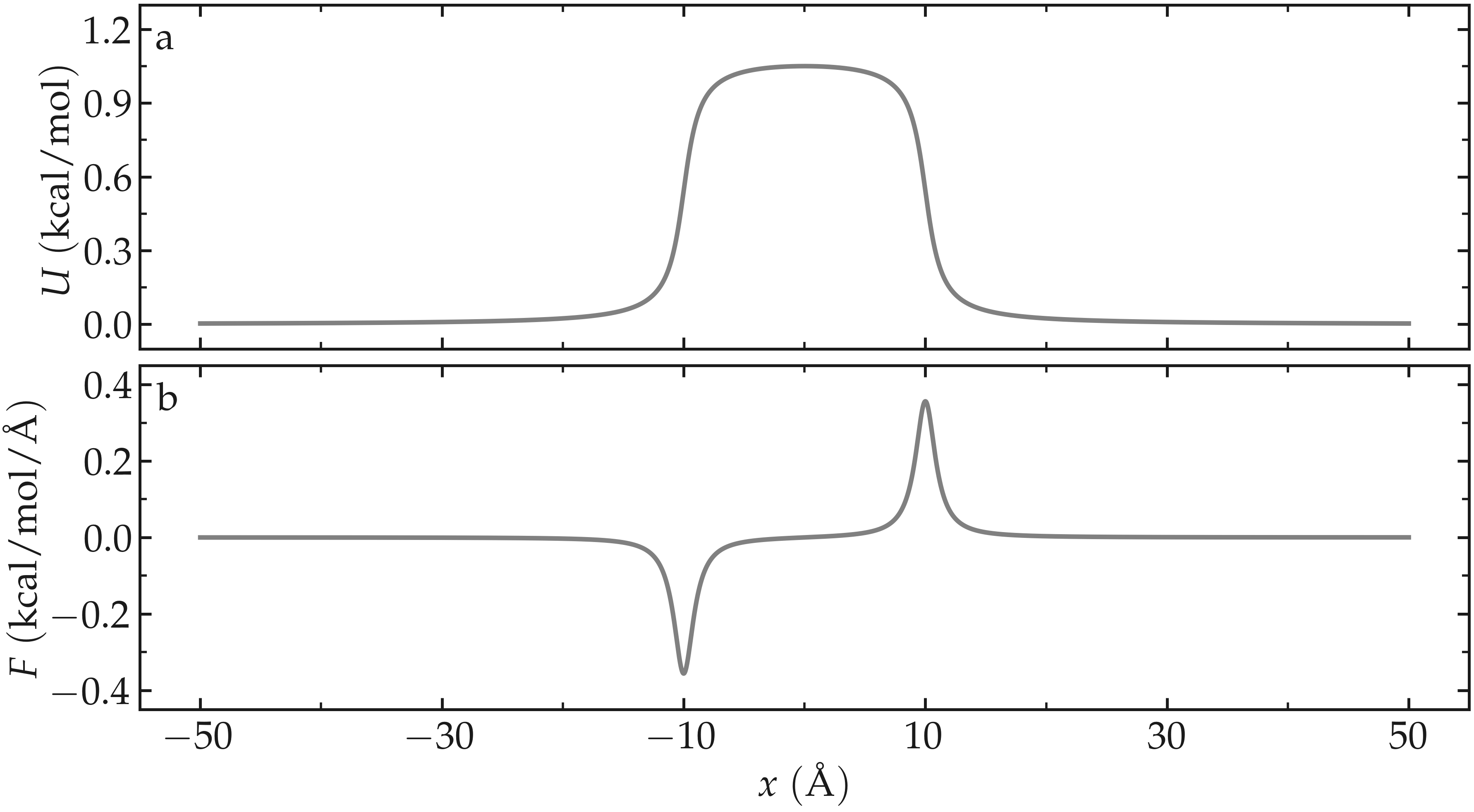
Figure: Potential \(U\) given in Eq. (2) (a) and force \(F\) given in Eq. (3) (b) as functions of the coordinate \(x\). Here, \(U_0 = 0.36~\text{kcal/mol}\), \(\delta = 1.0~\text{Å}\), and \(x_0 = 10~\text{Å}\).
We impose the force \(F(x)\) to the atoms in the simulation
using the fix addforce command. Add the following
lines to free-sampling.lmp:
variable U atom ${U0}*atan((x+${x0})/${dlt})-${U0}*atan((x-${x0})/${dlt})
variable F atom ${U0}/((x-${x0})^2/${dlt}^2+1)/${dlt}-${U0}/((x+${x0})^2/${dlt}^2+1)/${dlt}
fix myadf all addforce v_F 0.0 0.0 energy v_U
Next, we combine the fix nve with a fix langevin thermostat:
fix mynve all nve
fix mylgv all langevin 119.8 119.8 500 30917
When combining these two commands, the MD simulation operates in the NVT ensemble, maintaining a constant number of atoms \(N\), constant volume \(V\), and a temperature \(T\) that fluctuates around a target value.
To ensure that the equilibration time is sufficient, we will track the evolution of
the number of atoms in the central - energetically unfavorable - region,
referred to as mymes, using the n_center variable:
region mymes block -${x0} ${x0} INF INF INF INF
variable n_center equal count(all,mymes)
thermo_style custom step temp etotal v_n_center
thermo 10000
For visualization, use one of the following options: the dump image command to
create .ppm images of the system, or the dump atom command to write a
VMD-compatible trajectory to a file:
# Option 1
dump viz1 all image 50000 myimage-*.ppm type type shiny 0.1 box yes 0.01 view 180 90 zoom 6 size 1600 500 fsaa yes
dump_modify viz1 backcolor white acolor 1 cyan adiam 1 3 boxcolor black
# Option 2
dump viz2 all atom 50000 free-sampling.lammpstrj
Finally, let us perform an equilibration of 50000 steps, using a timestep of \(2\,\text{fs}\), corresponding to a total duration of \(100\,\text{ps}\):
timestep 2.0
run 50000
Run the simulation with LAMMPS. The number of atoms in the central region, \(n_\mathrm{center}\), reaches its equilibrium value after approximately \(40\,\text{ps}\).
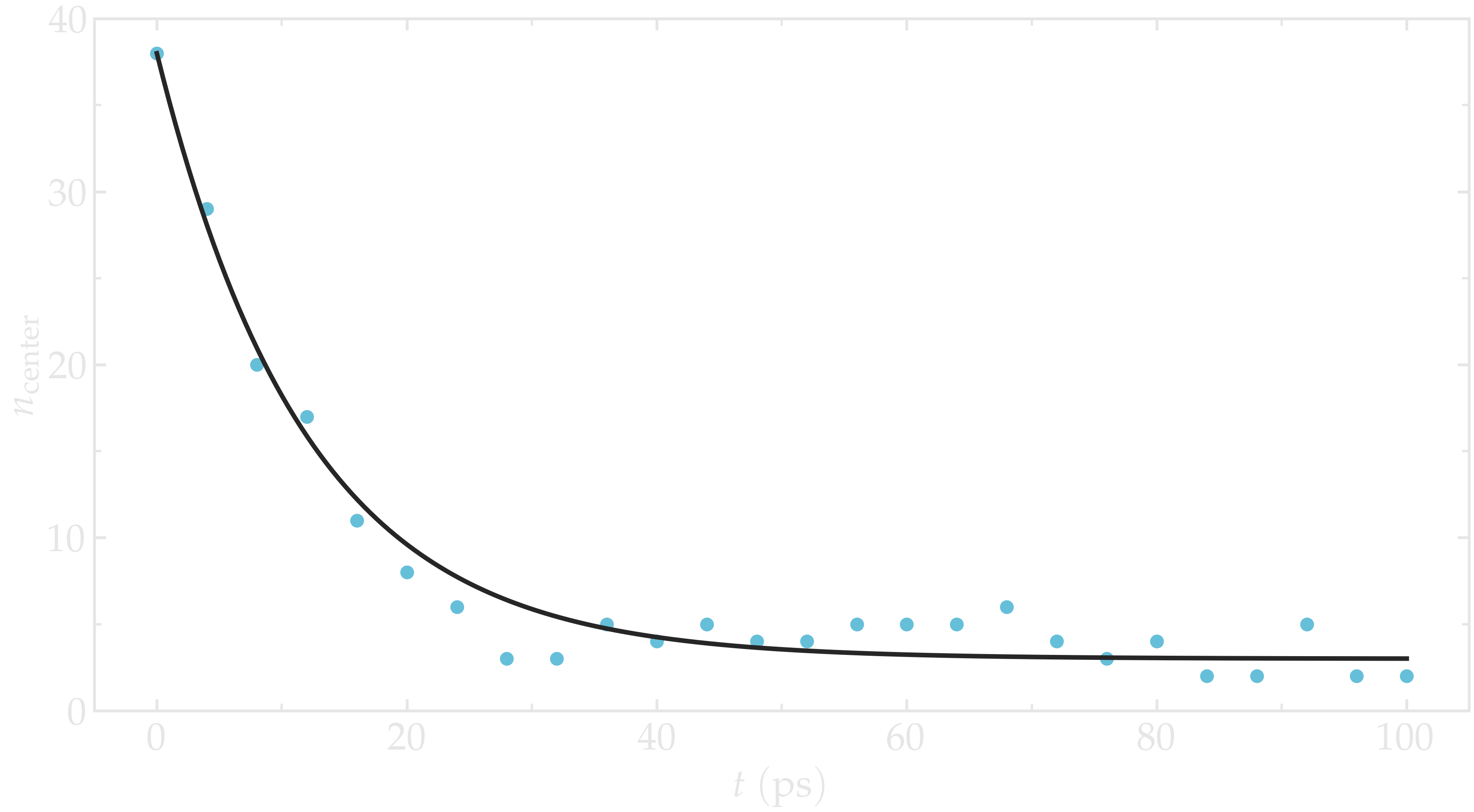
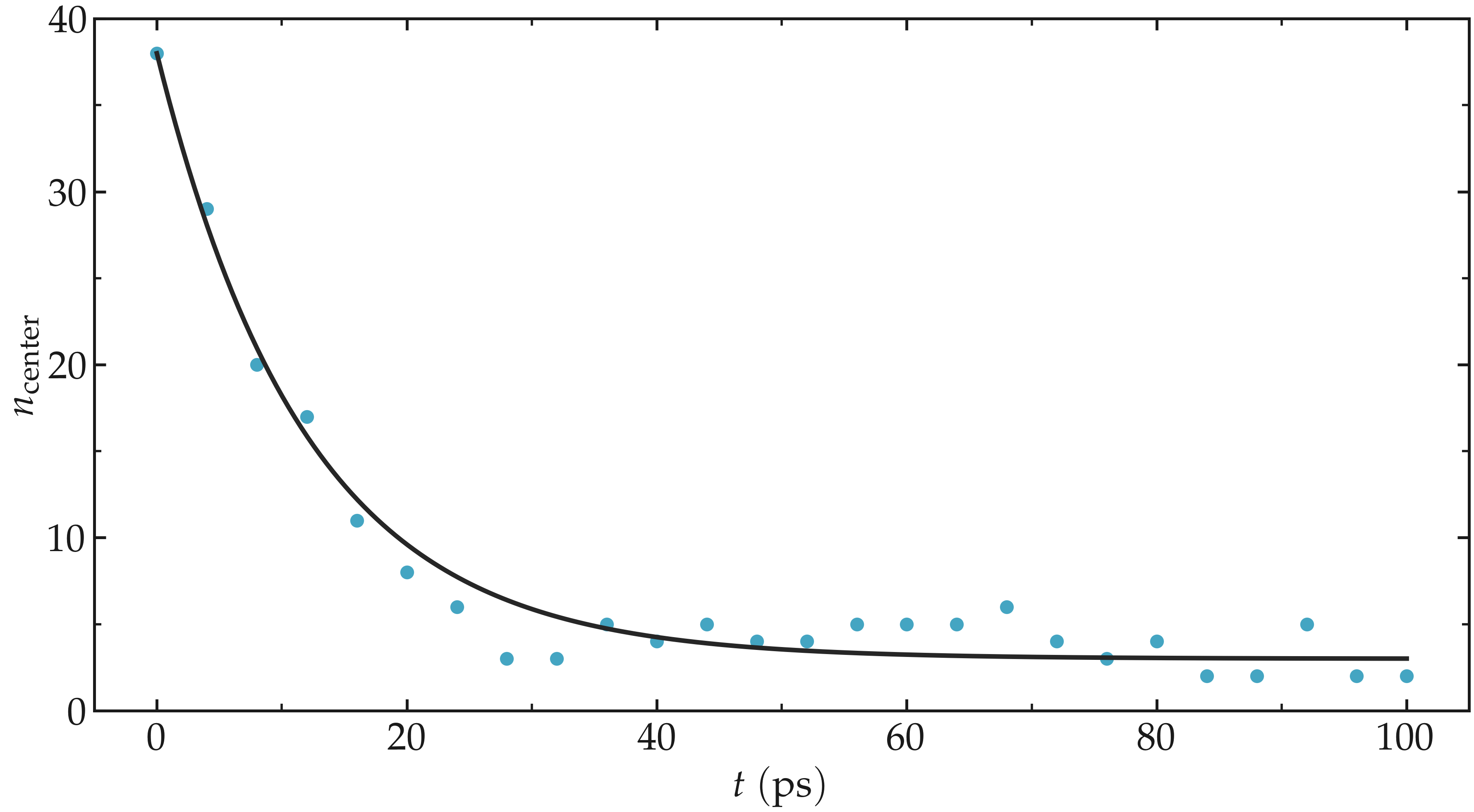
Figure: Evolution of the number of atoms \(n_\text{center}\) in the central
region mymes as a function of time \(t\) during equilibration. The dark line
is \(n_\text{center} = 22 \exp(-t/160)+5\) and serves as a guide for the eyes.
Here, \(U_0 = 0.36~\text{kcal/mol}\), \(\delta = 1.0~\text{Å}\), and \(x_0 = 10~\text{Å}\).
Run and data acquisition¶
Once the system is equilibrated, we will record the density profile of
the atoms along the \(x\)-axis using the ave/chunk command.
Add the following line to free-sampling.lmp:
# undump viz2 # Uncomment this line if you're using Option 2
reset_timestep 0
thermo 200000
compute cc1 all chunk/atom bin/1d x 0.0 2.0
fix myac all ave/chunk 100 20000 2000000 cc1 density/number file free-sampling.dat
run 2000000
The step count is reset to 0 using reset_timestep to synchronize it
with the output times of fix density/number. Run the simulation using
LAMMPS.
Figure: Snapshot of the system simulated during the free sampling step of the tutorial.
The atoms density is the lowest in the central part of the box, mymes. Here,
\(U_0 = 0.36~\text{kcal/mol}\), \(\delta = 1.0~\text{Å}\), and \(x_0 = 10~\text{Å}\).
Data analysis¶
Once the simulation is complete, the density profile from free-sampling.dat shows that the density in the center of the box is about two orders of magnitude lower than inside the reservoir. Next, we plot \(-R T \ln(\rho/\rho_\mathrm{bulk})\) (i.e. Eq. (1) where the pressure ratio \(p/p_\mathrm{bulk}\) is replaced by the density ratio \(\rho/\rho_\mathrm{bulk}\), assuming the system behaves as an ideal gas) and compare it with the imposed potential \(U\) from Eq. (2). The reference density, \(\rho_\text{bulk} = 0.0009~\text{Å}^{-3}\), was estimated by measuring the density of the reservoir from the raw density profiles. The agreement between the MD results and the imposed energy profile is excellent, despite some noise in the central part, where fewer data points are available due to the repulsive potential.
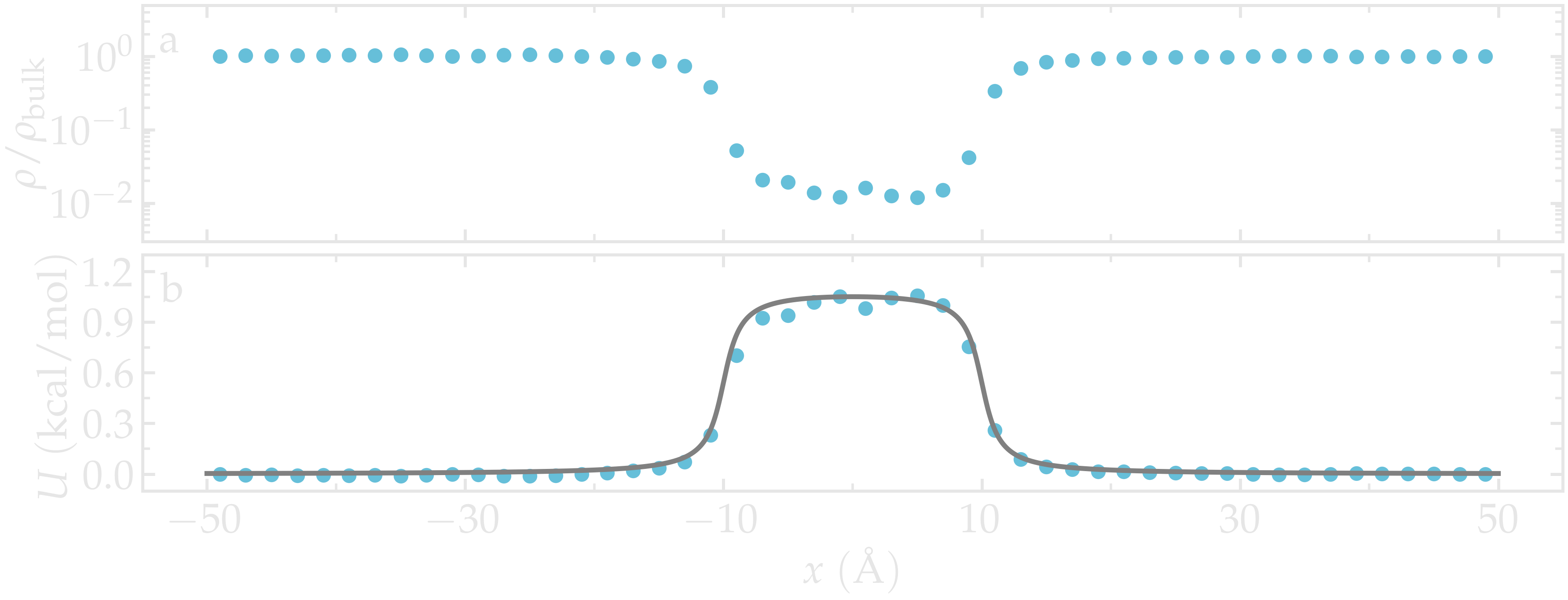
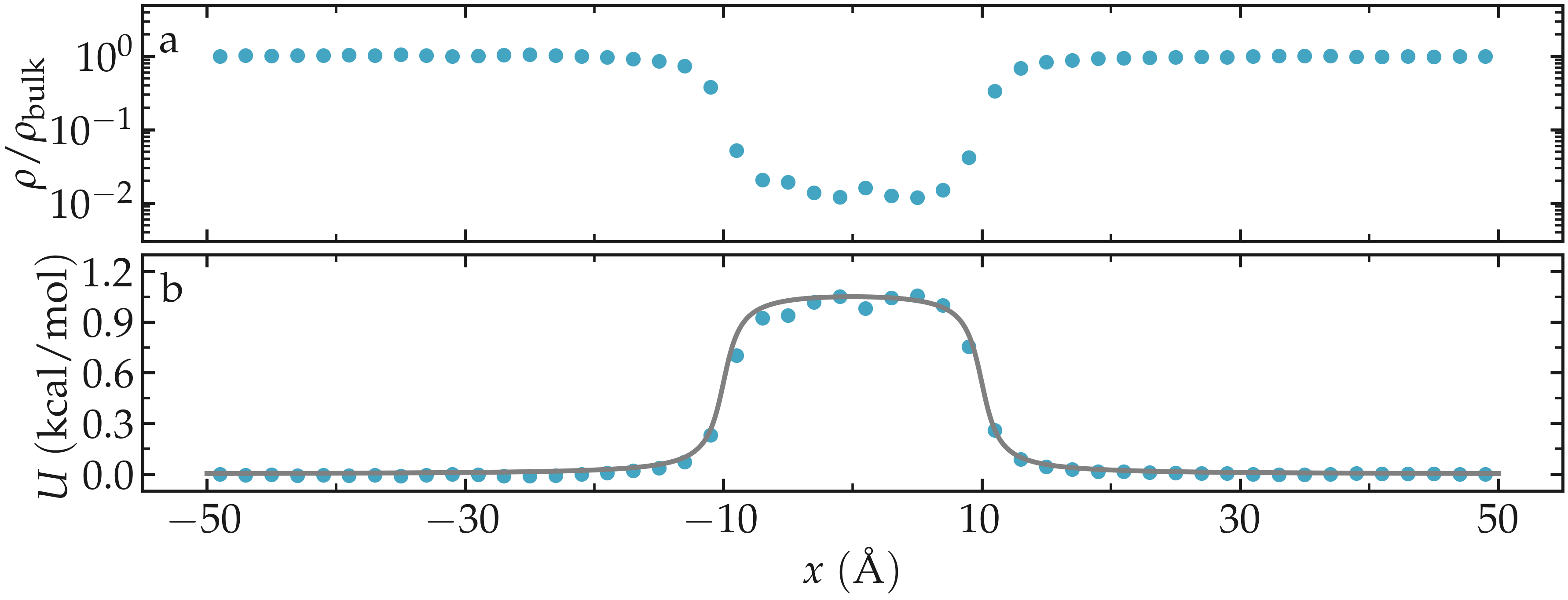
Figure: a) Fluid density, \(\rho\), along the \(x\) direction. b) Potential, \(U\), as a function of \(x\) measured using free sampling (disks) compared to the imposed potential given in Eq. (2) (line). Here, \(U_0 = 0.36~\text{kcal/mol}\), \(\delta = 1.0~\text{Å}\), \(x_0 = 10~\text{Å}\), and the measured reference density in the reservoir is \(\rho_\text{bulk} = 0.0009~\text{Å}^{-3}\).
The limits of free sampling¶
Increasing the value of \(U_0\) reduces the average number of atoms in the central region, making it difficult to achieve a high-resolution free energy profile. For example, running the same simulation with \(U_0 = 10 \epsilon\), corresponding to \(U_0 \approx 10 k_\text{B} T\), results in no atoms exploring the central part of the simulation box during the simulation. In such a case, employing an enhanced sampling method is recommended, as done in the next section.
Method 2: Umbrella sampling¶
Umbrella sampling is a biased molecular dynamics method in which additional forces are added to a chosen atom to force it to explore the more unfavorable areas of the system [6, 7, 45]. Here, to encourage one of the atoms to explore the central region of the box, we apply a potential \(V\) and force it to move along the \(x\)-axis. The chosen path is called the axis of reaction. Several simulations (called windows) will be conducted with varying positions for the center of the applied biasing. The results will be analyzed using the weighted histogram analysis method (WHAM) [52, 53], which allows for the removal of the biasing effect and ultimately deduces the unbiased free energy profile.
LAMMPS input script¶
If you are using LAMMPS–GUI, open the file named umbrella-sampling.lmp. Alternatively, if you are not using LAMMPS–GUI, create a new input file and paste in the following content:
variable sigma equal 3.405
variable epsilon equal 0.238
variable U0 equal 10*${epsilon}
variable dlt equal 1.0
variable x0 equal 10
variable k equal 0.5
units real
atom_style atomic
pair_style lj/cut 3.822
pair_modify shift yes
boundary p p p
The first difference from the previous case is the larger value for the repulsive potential \(U_0\), which makes the central area of the system very unlikely to be visited by free particles. The second difference is the introduction of the variable \(k\), which will be used for the biasing potential.
Let us create a simulation box with two atom types, including a single particle of type 2, by adding the following lines to umbrella-sampling.lmp:
region myreg block -50 50 -15 15 -50 50
create_box 2 myreg
create_atoms 2 single 0 0 0
create_atoms 1 random 199 34134 myreg overlap 3 maxtry 50
Next, we assign the same mass and LJ parameters to both atom types
1 and 2, and place the atoms of type 2 into a group named topull:
mass * 39.948
pair_coeff * * ${epsilon} ${sigma}
group topull type 2
Then, the same potential \(U\) and force \(F\) are applied to all the atoms,
together with the same fix nve and fix langevin commands:
variable U atom ${U0}*atan((x+${x0})/${dlt})-${U0}*atan((x-${x0})/${dlt})
variable F atom ${U0}/((x-${x0})^2/${dlt}^2+1)/${dlt}-${U0}/((x+${x0})^2/${dlt}^2+1)/${dlt}
fix myadf all addforce v_F 0.0 0.0 energy v_U
fix mynve all nve
fix mylgv all langevin 119.8 119.8 500 30917
Next, we perform a brief equilibration to prepare for the umbrella sampling run:
thermo 5000
# Option 1
dump viz1 all image 50000 myimage-*.ppm type type shiny 0.1 box yes 0.01 view 180 90 zoom 6 size 1600 500 fsaa yes
dump_modify viz1 backcolor white acolor 1 cyan acolor 2 red adiam 1 3 adiam 2 3 boxcolor black
# Option 2
dump viz2 all atom 50000 umbrella-sampling.lammpstrj
timestep 2.0
run 50000
So far, our code resembles that of Method 1, except for the additional particle of type 2. Particles of types 1 and 2 are identical, with the same mass and LJ parameters. However, the particle of type 2 will also be exposed to the biasing potential \(V\), which forces it to explore the central part of the box.
Now, we create a loop with 15 steps and progressively move the center of the bias potential by increments of 0.4 nm. Add the following lines to umbrella-sampling.lmp:
variable a loop 15
label loop
variable xdes equal 4*${a}-32
variable xave equal xcm(topull,x)
fix mytth topull spring tether ${k} ${xdes} 0 0 0
run 20000
fix myat1 all ave/time 10 10 100 v_xave v_xdes file umbrella-sampling.${a}.dat
run 200000
unfix myat1
next a
jump SELF loop
The spring command imposes the additional harmonic potential \(V\) with
the previously defined spring constant \(k\). The center of the harmonic
potential, \(x_\text{des}\), successively takes values
from \(-28\,\text{Å}\) to \(28\,\text{Å}\). For each value of \(x_\text{des}\),
an equilibration step of 40 ps is performed, followed by a step
of 400 ps during which the position of the particle of
type 2 along the \(x\)-axis, \(x_\text{ave}\), is saved in data files named umbrella-sampling.i.dat,
where \(i\) ranges from 1 to 15. Run the umbrella-sampling.lmp file using LAMMPS.
Note
The value of \(k\) should be chosen with care: if \(k\) is too small the particle won’t follow the biasing potential, and if \(k\) is too large there will be no overlapping between the different windows, leading to poor reconstruction of the free energy profile. See the section Side note: On the choice of k.
WHAM algorithm¶
To generate the free energy profile from the particle positions saved in
the umbrella-sampling.i.dat files, we use the
WHAM [52, 53] algorithm as implemented
by Alan Grossfield [54]. You can download it
from Alan Grossfield’s website. Make sure you download the WHAM code version
2.1.0 or later which introduces the units command-line option
used below. The executable called wham generated by following
the instructions from the website must be placed next to
umbrella-sampling.lmp. To apply the WHAM algorithm to our
simulation, we need a metadata file containing:
the paths to all the data files,
the values of \(x_\text{des}\),
the values of \(k\).
Download the umbrella-sampling.meta file and save it next to umbrella-sampling.lmp. Then, run the WHAM algorithm by typing the following command in the terminal:
./wham units real -30 30 50 1e-8 119.8 0 umbrella-sampling.meta umbrella-sampling.dat
where -30 and 30 are the boundaries, 50 is the number of bins, 1e-8 is the tolerance, and 119.8 is the temperature in Kelvin. A file called umbrella-sampling.dat is created, containing the free energy profile in kcal/mol. The resulting PMF can be compared with the imposed potential \(U\), showing excellent agreement.
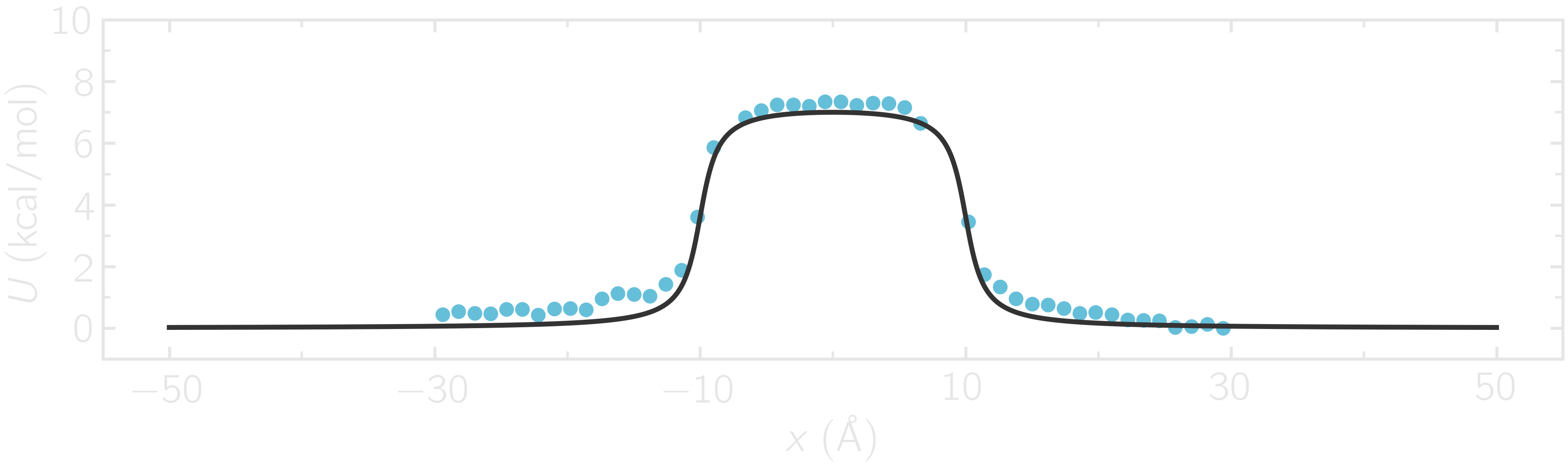
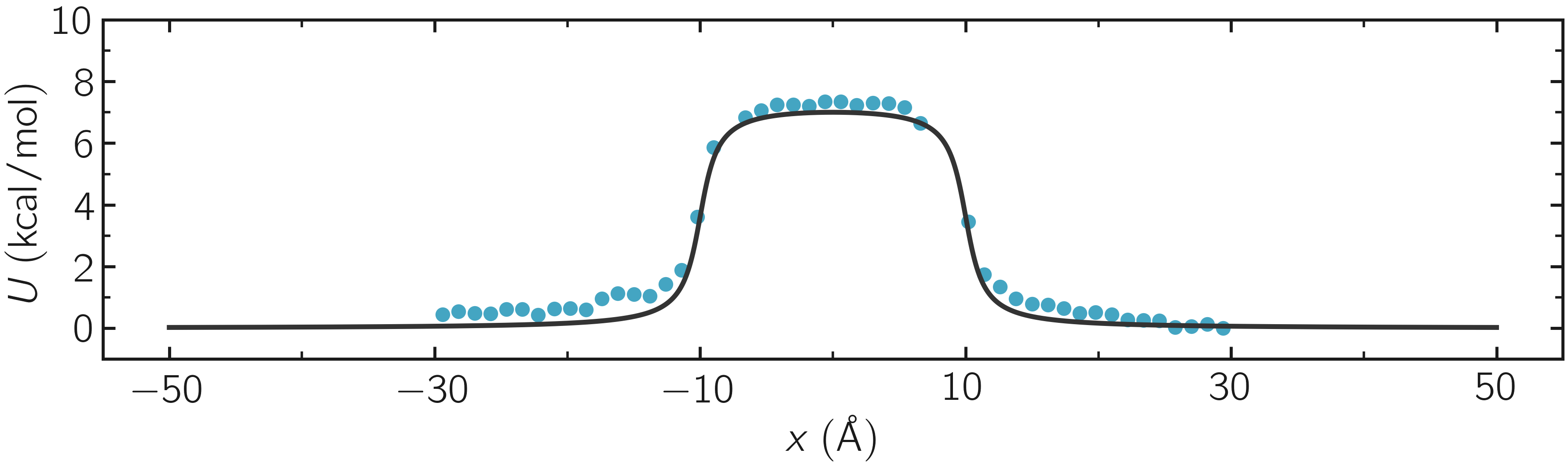
Figure: The potential, \(U\), as a function of \(x\), measured using umbrella sampling (disks), is compared to the imposed potential given in Eq. (2) (line). Parameters are \(U_0 = 2.38~\text{kcal/mol}\), \(\delta = 1.0~\text{Å}\), and \(x_0 = 10~\text{Å}\).
Remarkably, this excellent agreement is achieved despite the very short calculation time and the high value for the energy barrier. Achieving similar results through free sampling would require performing extremely long and computationally expensive simulations.
Side note: On the choice of \(k\)¶
One difficult part of umbrella sampling is choosing the value of \(k\). Ideally, you want the biasing potential to be strong enough to force the chosen atom or molecule to move along the chosen axis, while also allowing fluctuations in its position large enough to ensure some overlap in the probability density between neighboring positions. Here, as an illustration, three different values of \(k\) are tested:
If \(k\) is too small, the biasing potential is too weak to force the particle to explore the region of interest, making it impossible to reconstruct the PMF (see panel a in the figure below).
If \(k\) is “appropriate”, the particle explores the entire axis, and the probability distributions are strongly impacted by the potential one wants to probe, as shown in panel b.
If \(k\) is too large, the biasing potential dominates over the potential one wants to probe, which reduces the sensitivity of the method (panel c).
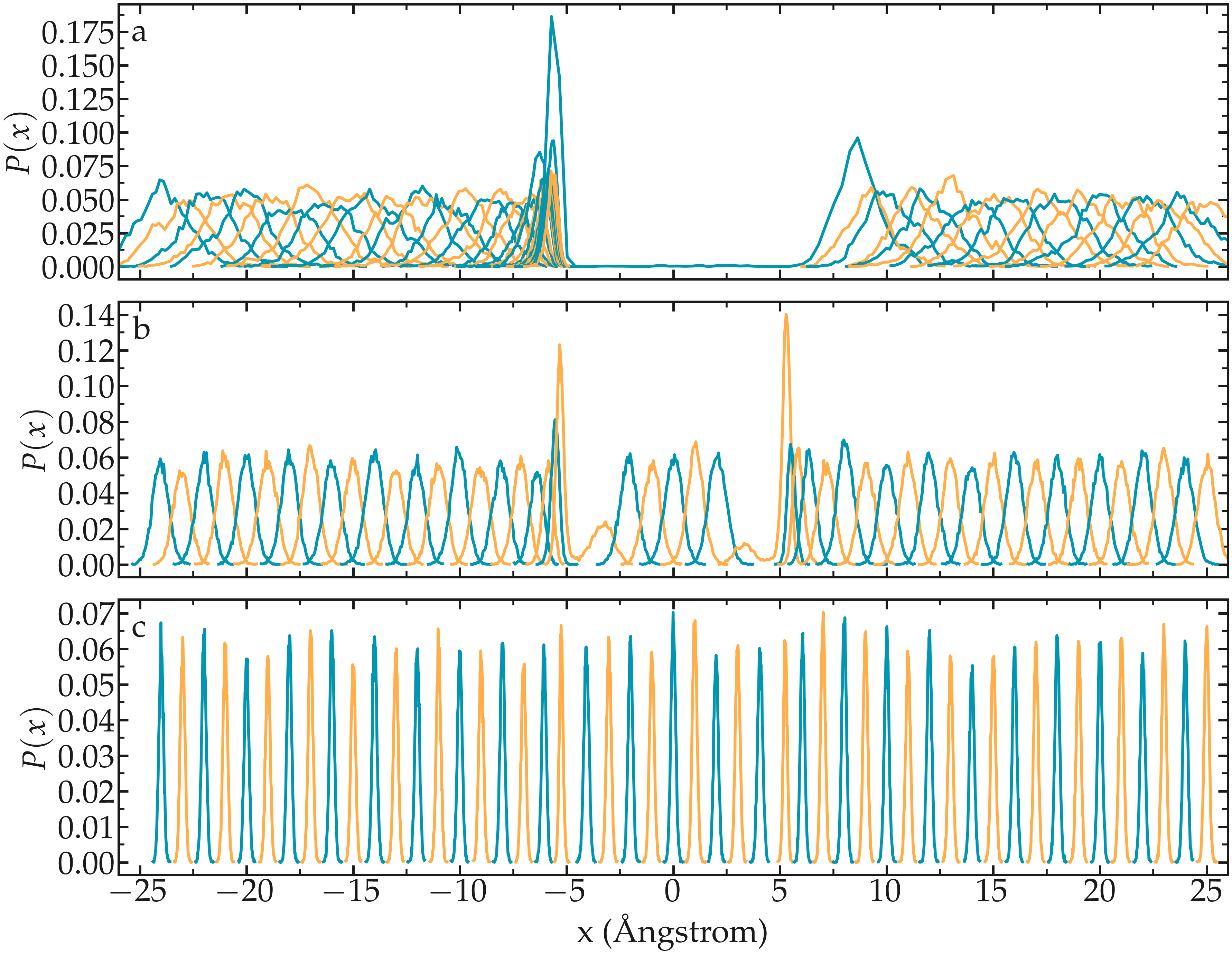
Figure: Probability density for each run with \(k = 0.15\,\text{kcal}/\text{mol}/\mathrm{Å}^2\) (a) (a value that is too small to bring the particle into the central region), \(k = 1.5\,\text{kcal}/\text{mol}/\mathrm{Å}^2\) (b) (a value that allows the particle to explore the entire path), and \(k = 15\,\text{kcal}/\text{mol}/\mathrm{Å}^2\) (c) (a value so strong that it becomes difficult to perceive the effect of the probed potential).